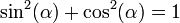Difference between revisions of "Matlab Arrays"
m (→Elemental Multiplication) |
m |
||
| Line 1: | Line 1: | ||
[[Category:Matlab]] | [[Category:Matlab]] | ||
| + | |||
== Array Basics == | == Array Basics == | ||
| + | |||
An array is an ''n''-dimensional collection of numbers. [[LinearAlgebra#Basics: Matrices & Vectors|Matrices]] are 2-dimensional arrays, and [[LinearAlgebra#Basics: Matrices & Vectors|vectors]] are 1-dimensional arrays. | An array is an ''n''-dimensional collection of numbers. [[LinearAlgebra#Basics: Matrices & Vectors|Matrices]] are 2-dimensional arrays, and [[LinearAlgebra#Basics: Matrices & Vectors|vectors]] are 1-dimensional arrays. | ||
| Line 36: | Line 38: | ||
</center> | </center> | ||
Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | ||
| + | |||
== Creating Arrays in Matlab == | == Creating Arrays in Matlab == | ||
| + | In this section we will discuss several ways of creating arrays (matrices and vectors) in MATLAB. | ||
=== Manual Creation === | === Manual Creation === | ||
| + | |||
Often we need to create small arrays with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. For example, to create the '''column vector ''' | Often we need to create small arrays with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. For example, to create the '''column vector ''' | ||
<center><math> | <center><math> | ||
| Line 88: | Line 93: | ||
A = [ acol1 acol2 ]; | A = [ acol1 acol2 ]; | ||
</source> | </source> | ||
| + | |||
=== Using the ":" operator to create arrays === | === Using the ":" operator to create arrays === | ||
| + | |||
Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The ''':''' operator (see [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/colon.html&http://www.mathworks.com/access/helpdesk/help/techdoc/ref/linspace.html here] for MATLAB's explanation of this) can help us create such arrays: | Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The ''':''' operator (see [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/colon.html&http://www.mathworks.com/access/helpdesk/help/techdoc/ref/linspace.html here] for MATLAB's explanation of this) can help us create such arrays: | ||
| Line 110: | Line 117: | ||
h = (1:3)'; % creates a column vector with elements 1, 2, 3. | h = (1:3)'; % creates a column vector with elements 1, 2, 3. | ||
</source> | </source> | ||
| + | |||
=== Linspace and Logspace === | === Linspace and Logspace === | ||
| + | |||
Occasionally we want to create numbers that are equally spaced between two limits. We can use the [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/linspace.html&http://www.mathworks.com/access/helpdesk/help/techdoc/ref/logspace.html linspace] command to do this. | Occasionally we want to create numbers that are equally spaced between two limits. We can use the [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/linspace.html&http://www.mathworks.com/access/helpdesk/help/techdoc/ref/logspace.html linspace] command to do this. | ||
; linspace( lo, hi, n ); | ; linspace( lo, hi, n ); | ||
| Line 143: | Line 152: | ||
d = logspace(-3,3); % 50 points between 10^-3 and 10^3. | d = logspace(-3,3); % 50 points between 10^-3 and 10^3. | ||
</source> | </source> | ||
| + | |||
=== Shortcuts for Special Matrices === | === Shortcuts for Special Matrices === | ||
| Line 166: | Line 176: | ||
; '''rand'''(nrow,ncol) [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/rand.html&http://www.mathworks.com/access/helpdesk/help/techdoc/learn_matlab/f2-644.html] | ; '''rand'''(nrow,ncol) [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/rand.html&http://www.mathworks.com/access/helpdesk/help/techdoc/learn_matlab/f2-644.html] | ||
: creates an array with ''nrow'' rows and ''ncol'' columns full of random numbers. | : creates an array with ''nrow'' rows and ''ncol'' columns full of random numbers. | ||
| + | |||
=== Sparse Matrices === | === Sparse Matrices === | ||
{{Stub|section}} | {{Stub|section}} | ||
| + | |||
== Array Arithmetic == | == Array Arithmetic == | ||
| + | |||
One of the most powerful features of MATLAB is the ability to perform operations on entire arrays at once. | One of the most powerful features of MATLAB is the ability to perform operations on entire arrays at once. | ||
=== Addition and Subtraction === | === Addition and Subtraction === | ||
| + | |||
Given two arrays '''of the same size''', one may add or subtract these as follows: | Given two arrays '''of the same size''', one may add or subtract these as follows: | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| Line 203: | Line 217: | ||
b = a + A(1,:); | b = a + A(1,:); | ||
</source> | </source> | ||
| + | |||
=== Multiplication === | === Multiplication === | ||
| + | |||
Multiplication of two arrays, '''C=A*B''' requires that the number of columns in A is equal to the number of rows in B. The array '''C''' has the same number of rows as '''A''' and same number of columns as '''B'''. | Multiplication of two arrays, '''C=A*B''' requires that the number of columns in A is equal to the number of rows in B. The array '''C''' has the same number of rows as '''A''' and same number of columns as '''B'''. | ||
| Line 226: | Line 242: | ||
</source> | </source> | ||
C is a 3x2 array (3 rows, 2 columns) | C is a 3x2 array (3 rows, 2 columns) | ||
| − | |||
| Line 285: | Line 300: | ||
==== Elemental Division ==== | ==== Elemental Division ==== | ||
| + | |||
The '''. /''' operator performs elemental division on two arrays of the ''same size''. | The '''. /''' operator performs elemental division on two arrays of the ''same size''. | ||
| Line 305: | Line 321: | ||
==== Elemental Exponentiation ==== | ==== Elemental Exponentiation ==== | ||
| + | |||
'''A .^ b''' results in each element in '''A''' being raised to the power '''b'''. Here '''b''' must be a scalar, ''not'' a matrix or a vector. | '''A .^ b''' results in each element in '''A''' being raised to the power '''b'''. Here '''b''' must be a scalar, ''not'' a matrix or a vector. | ||
| Line 327: | Line 344: | ||
<math>C = \begin{bmatrix} 37 & 54 \\ 81 & 118 \end{bmatrix} </math>. | <math>C = \begin{bmatrix} 37 & 54 \\ 81 & 118 \end{bmatrix} </math>. | ||
Here we have C=A*A*A, where these are matrix-matrix multiplications. | Here we have C=A*A*A, where these are matrix-matrix multiplications. | ||
| + | |||
== Accessing Arrays == | == Accessing Arrays == | ||
| + | |||
Often we need to access certain elements or groups of elements from an array. There are a few ways to do this. | Often we need to access certain elements or groups of elements from an array. There are a few ways to do this. | ||
=== Indexing arrays === | === Indexing arrays === | ||
| + | |||
Recall that an array is simply a collection of numbers. Arrays may be 1-dimensional (vectors), 2-dimensional (matrices) or even higher dimensional. Each number in an array has a unique location identified by an ''index''. Array indexing is best illustrated by example. | Recall that an array is simply a collection of numbers. Arrays may be 1-dimensional (vectors), 2-dimensional (matrices) or even higher dimensional. Each number in an array has a unique location identified by an ''index''. Array indexing is best illustrated by example. | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| Line 354: | Line 374: | ||
=== Slicing arrays using the ":" operator === | === Slicing arrays using the ":" operator === | ||
| + | |||
Sometimes we need to grab a group of elements from an array. We can do this using the ''':''' operator For example: | Sometimes we need to grab a group of elements from an array. We can do this using the ''':''' operator For example: | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| Line 389: | Line 410: | ||
; min | ; min | ||
: Analogous to '''max'''. | : Analogous to '''max'''. | ||
| + | |||
=== Other Useful Tools === | === Other Useful Tools === | ||
| + | |||
Use MATLAB's help command to learn more about how to use these commands. | Use MATLAB's help command to learn more about how to use these commands. | ||
Revision as of 07:22, 25 August 2008
Array Basics
An array is an n-dimensional collection of numbers. Matrices are 2-dimensional arrays, and vectors are 1-dimensional arrays.
Vectors can be either a row or column vector:
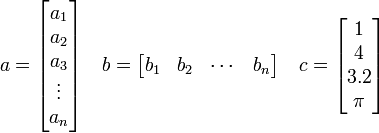
We refer to the elements of an array by their position in the array. For example, the third element in  is 3.2, and the second element in
is 3.2, and the second element in 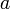 is
is 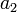 .
.
Matrices are two-dimensional arrays, whose elements are referred to by the row and column that they belong to. For example,
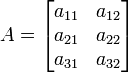
is a matrix with three rows and two columns. We refer to this as a 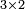 matrix. The first index refers to the row and the second index refers to the column.
matrix. The first index refers to the row and the second index refers to the column.
Transposing Arrays
Occasionally we want to transpose an array. This is done by exchanging rows and columns. For example,
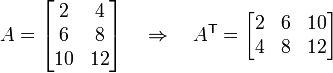
Here the 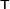 superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words,
superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, 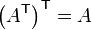 .
.
Creating Arrays in Matlab
In this section we will discuss several ways of creating arrays (matrices and vectors) in MATLAB.
Manual Creation
Often we need to create small arrays with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. For example, to create the column vector
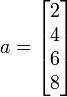
we could use any of the following Matlab commands:
a = [ 2; 4; 6; 8; ]; % create a column vector
a = [ 2 4 6 8 ]'; % create a row vector and then
% transpose it to produce a column vector.
a = [ 2
4
6
8 ]; % creates a column vector.
Note that the semicolon (;) identifies the end of a row in the matrix. Commas may be used to separate columns in the matrix, but they are not necessary.
A row vector such as b = [1 3 5 7 ] may be created as
b = [ 1 3 5 7 ];
b = [ 1, 3, 5, 7 ];
b = [ 1; 3; 5; 7 ]'; % transpose a column vector.
Matrices may be created directly in much the same way as vectors are. As an example, let's build the matrix
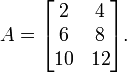
This may be done in several ways.
A = [ 2 4; 6 8; 10 12 ];
A = [ 2 4
6 8
10 12 ];
Note that a semicolon (;) separates each row of the matrix while spaces separate each column.
We may also create a matrix from vectors. For example, we may construct A from its rows as follows:
arow1 = [ 2 4 ];
arow2 = [ 6 8 ];
arow3 = [ 10 12 ];
A = [ arow1; arow2; arow3 ];
Similarly, we can build a matrix from its columns:
acol1 = [2 6 10]';
acol2 = [4; 8; 12];
A = [ acol1 acol2 ];
Using the ":" operator to create arrays
Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The : operator (see here for MATLAB's explanation of this) can help us create such arrays:
array = lower : increment : upper;
This creates an array starting at lower and ending at upper with spacing of increment. You may eliminate the increment argument, in which case it defaults to 1.
Examples:
a = 1:5; % creates a=[ 1 2 3 4 5 ]
b = 1:1:5; % creates b=[ 1 2 3 4 5 ]
c = 1:2:7; % creates c=[ 1 3 5 7 ]
d = 1:2:8; % creates d=[ 1 3 5 7 ]
e = 1.1:5 % creates e=[ 1.1 2.3 3.1 4.1 ]
f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ]
g = 5:-1:1; % creates g=[ 5 4 3 2 1 ];
h = (1:3)'; % creates a column vector with elements 1, 2, 3.
Linspace and Logspace
Occasionally we want to create numbers that are equally spaced between two limits. We can use the linspace command to do this.
- linspace( lo, hi, n );
- Creates a row vector with n points equally spaced between lo and hi.
- The last argument, n is not required. If omitted, 100 points will be used.
Examples:
a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ]
b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ]
c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ]
d = linspace(1,5,5)'; % creates a column vector
e = linspace(1,5); % uses 100 points between 1 and 5.
lo=0; hi=10;
f = linspace(lo,hi); % uses 100 points between lo (0) and hi (10)
Sometimes we want points logarithmically spaced. For example, we may want to create a vector a=[ 0.1 1 10 100]. This can be accomplished using the logspace command:
-
logspace( lo, hi, n );
- Creates a vector with n points spaced logarithmically between
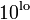 and
and 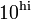
- The last argument, n is not required. If omitted, 50 points will be used.
Examples:
a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ]
b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ]
c = logspace(-1,3,5)'; % creates a column vector
d = logspace(-3,3); % 50 points between 10^-3 and 10^3.
Shortcuts for Special Matrices
- ones(nrow,ncol) [1]
- creates an array of all ones with nrow rows and ncol columns.
- zeros(nrow,ncol) [2]
- creates an array of all zeros with nrow rows and ncol columns.
- eye(nrow,ncol) [3]
- creates an array with ones on its diagonal and zeros elsewhere.
- Example: eye(3,2) produces
 while eye(3,3) gives
while eye(3,3) gives 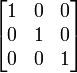
- rand(nrow,ncol) [4]
- creates an array with nrow rows and ncol columns full of random numbers.
Sparse Matrices
|
Array Arithmetic
One of the most powerful features of MATLAB is the ability to perform operations on entire arrays at once.
Addition and Subtraction
Given two arrays of the same size, one may add or subtract these as follows:
C = A + B;
Example 1:
A = rand(3);
B = ones(3);
C = A+B;
D = B + eye(3);
Example 2:
a = [1 2 3];
b = [4 5 6];
c = a+b;
d = a' + b';
Example 3:
A = [1 2 3; 4 5 6];
a = [-1 -2 -3];
b = a + A(1,:);
Multiplication
Multiplication of two arrays, C=A*B requires that the number of columns in A is equal to the number of rows in B. The array C has the same number of rows as A and same number of columns as B.
Example 1 - Here A and B are the same size:
A = rand(3); B = rand(3);
C = A*B;
Example 2 - Here b is a vector and the product is also a vector.
A = rand(3); b = rand(3,1);
c = A*B;
Example 3 - Here A and B are both matrices, but of different size.
A = rand(3,5);
B = rand(5,2);
C = A*B;
C is a 3x2 array (3 rows, 2 columns)
Elemental Operations
The following table summarizes the elemental operators available in MATLAB. Each of these operators is discussed in more detail below.
| Operator | Description |
|---|---|
| .* | Elemental Multiplication |
| ./ | Elemental Division |
| .^ | Elemental Exponentiation |
Elemental Multiplication
Arrays of the same size may be multiplied or divided element-by-element using the .* operator so that C = A .* B produces an array whose elements are given by 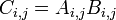 .
.
Example 1:
A = [1 2; 3 4];
B = 2*ones(2);
C = A .* B
This results in 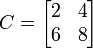
Example 2:
a = [1 2 3];
b = [2; 4; 6];
c = a .* b';
This results in 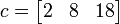 .
Note that elemental multiplication is very different from array multiplication. For example,
.
Note that elemental multiplication is very different from array multiplication. For example,
d = a*b;
e = b*a;
would produce d = 24, and
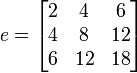 .
.
If you need to brush up on this, see the tutorial on matrix multiplication.
Elemental Division
The . / operator performs elemental division on two arrays of the same size.
Example 1:
a = [ 2 4 6 ];
b = [ 1 2 3 ];
c = a./b;
d = b./a;
results in c=[2 2 2] and d=[0.5 0.5 0.5].
Example 2:
A = [1 2 3; 4 5 6];
B = rand(2,3);
C = A./B;
D = B./A;
Elemental Exponentiation
A .^ b results in each element in A being raised to the power b. Here b must be a scalar, not a matrix or a vector.
Example 1:
x = linspace(-pi,pi);
y = sin(x);
z = cos(x);
w = y.^2 + z.^2;
Here all elements of w should be equal to 1.
NOTE: Elemental exponentiation is very different from array exponentiation. For example:
A = [1 2; 3 4];
B = A.^3;
C = A^3;
results in
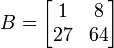 and
and
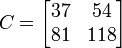 .
Here we have C=A*A*A, where these are matrix-matrix multiplications.
.
Here we have C=A*A*A, where these are matrix-matrix multiplications.
Accessing Arrays
Often we need to access certain elements or groups of elements from an array. There are a few ways to do this.
Indexing arrays
Recall that an array is simply a collection of numbers. Arrays may be 1-dimensional (vectors), 2-dimensional (matrices) or even higher dimensional. Each number in an array has a unique location identified by an index. Array indexing is best illustrated by example.
a = 2:2:10; % creates a row vector: [2 4 6 8 10]
a1 = a(1); % assigns the first element of a to "a1"
We can likewise index into a matrix as:
B = [ 5 2 9; 1 7 3; 2 6 0];
var = B(2,3); % var = 3 (row 2, column 3)
In general for a two-dimensional array, B(i,j) refers to the ith row and jth column of B. This is extensible to arrays of higher dimensions as well.
If we return to our previous example with the B matrix, we find something interesting:
B = [ 5 2 9; 1 7 3; 2 6 0];
b = B(5);
What should the value of b be? One might expect this to result in an error, since B is not a vector. However, this returns b=7. What is happening? Matlab actually treats a matrix as a long vector, B = [ 5 2 9 1 7 3 2 6 0 ], with each row stacked next to the previous row. Therefore, B(5) says "go to the fifth entry" counted along rows.
Slicing arrays using the ":" operator
Sometimes we need to grab a group of elements from an array. We can do this using the : operator For example:
A = [ 1 2 3; 4 5 6; 7 8 9 ];
col1 = A(:,1); % all rows, first column
row2 = A(2,:); % second row, all columns
Here : acts to select all elements in the row or column of A. We can grab a subset of rows or columns by the following:
A = [ 1 2 3; 4 5 6; 7 8 9 ];
a = A( 1:2, 2:3 );
This takes rows 1 and 2 and columns 2 and 3 in A and creates a new array a. Now a looks like 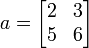 .
.
The : operator is a very powerful tool to extract portions of an array.
Information about Arrays
- size
- returns the number of rows and columns in an array. For example,
-
A = [1 2 3; 4 5 6];
-
[nrow,ncol] = size(A);
-
- The result of this is that nrow=2 and ncol=3.
- length
- returns the number of elements in a vector. Example:
-
a = [1 2 3 4 3 2 1];
-
na = length(a);
-
- Results in na=7.
- max
- For a vector, max(v) returns the largest element in v. For matrices, max(V) returns a row vector whose elements contain the maximum value in each column of V.
- min
- Analogous to max.
Other Useful Tools
Use MATLAB's help command to learn more about how to use these commands.
| Matlab command | Summary | Example(s) |
|---|---|---|
| sum |
|
a=sum([1 2 3]); % a=6
b=sum([1 2; 3 4]); % b = [4 6]
|
| sort | Sort an array in ascending or descending order. | sort([2 5 1]) % gives '''1 2 5'''
|
| any | any(A) Evaluates to "true" if any of the elements in the array are true (nonzero). |
a=[1 2 3]; b=[1 3 4];
r1 = any(a>b); % r1 is FALSE (equal to 0)
r2 = any(a==b); % r2 is TRUE (equal to 1) since a(1) is equal to b(1).
|
| all | Evaluates to "true" if all of the elements in the array are true (nonzero). |
A = [1 2; 3 4];
B = [-1 1; 2 3];
r1 = all(A>B); % r1 is TRUE (equal to 1) since the elements in A are
% all greater than their corresponding elements in B.
r2 = all(2*B>A); % r2 is FALSE
|
| find | find(A) returns the indices where A is nonzero. |
A = [1 5 0; 0 2 0];
i = find(A(:,1)); % i=1
i = find(A(:,2)); % i=[1 2]'
i = find(A); % i=[1 3 4]'
[i,j] = find(A); % i=[ 1 1 2 ]' j=[ 1 2 2 ]'
i = find(A>4); % i=3
[i,j] = find(A<2); % i=[1 2 1 2]' j=[1 1 3 3]'
|
| isequal | isequal(A,B) returns true if all elements of A and B are equal, false otherwise. |
A = [1 2; 3 4];
B = [2 4; 6 8];
c = isequal(A,B); % c is FALSE
d = isequal(2*A,B); % d is TRUE
Here is something a bit more complex, using the fact that x = rand(5);
y1 = sin(x).*sin(x);
z1 = cos(x).*cos(x);
q = ones(5);
c = isequal(q,y1+z1); % c is TRUE
|