Difference between revisions of "Matlab Basics"
(New page: == The Command Window == {{Stub|section}} === Defining Variables === {{Stub|section}} === Useful Commands === {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-a...) |
(→Basic Operations & Common Functions) |
||
| (22 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
== The Command Window == | == The Command Window == | ||
| − | |||
| − | == | + | MATLAB's command window can be used as a very powerful calculator. The <tt>>></tt> indicates that MATLAB is ready to accept a command. It works much like your calculator. For example, |
| − | + | >> 1 + cos(pi/2) | |
| + | ans = | ||
| + | 1 | ||
| + | >> 5^2 % square 5 | ||
| + | ans = | ||
| + | 25 | ||
| + | Note that anything following a <tt>%</tt> on a line is ignored. This allows us to include comments in our calculations. | ||
| + | == Defining Variables == | ||
| + | |||
| + | By using variables instead of numbers, our calculations look much like they would on paper. For example, from physics we know that projectile motion (in the absence of air resistance) is governed by the equations | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t) &= y(0) + v(0) \, t + \tfrac{1}{2} a \, t^2, \\ | ||
| + | v(t) &= v(0) + a\,t, | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | where <math>y(0)</math> and <math>v(0)</math> are the position and velocity of the projectile at time <math>t=0</math> and <math>a</math> is the acceleration. | ||
| + | |||
| + | === Example === | ||
| + | Assume that we have the following problem: | ||
| + | A bullet is shot upward with an initial velocity of 300 feet per second (fps). | ||
| + | Neglecting air resistance, determine the maximum height of the bullet. | ||
| + | The maximum height occurs when <math>v(t)=0</math>. We can solve the equation for <math>v(t)</math> to find | ||
| + | <center><math> | ||
| + | t=\frac{v(t)-v(0)}{a}. | ||
| + | </math></center> | ||
| + | This gives the time at which the bullet reaches its maximum height. We can then use the equation for <math>y(t)</math> to determine how high it is at that time. | ||
| + | |||
| + | Let's solve this in MATLAB. First we define the initial height, the initial velocity, and the acceleration. We also know the final velocity - it is zero. | ||
| + | <source lang="matlab"> | ||
| + | y0 = 0.0; % initial height (feet) | ||
| + | v0 = 300; % initial velocity (feet/s) | ||
| + | vt = 0.0; % final velocity (feet/s) | ||
| + | a = -32.2; % gravitational acceleration (feet^2/s) | ||
| + | </source> | ||
| + | Now we can define the time that the projectile reaches its maximum height, and then determine what the maximum height is. We use the variables we just defined: | ||
| + | <source lang="matlab"> | ||
| + | t = (vt-v0)/a; % time (s) when the bullet stops (maximum height) | ||
| + | yt = y0 + v0*t + a*t^2/2; % maximum height (feet). | ||
| + | </source> | ||
| + | If we omit the <tt>;</tt> on the line for <tt>yt</tt> MATLAB will print its value. Or we can simply type the variable and MATLAB will print it. Doing this we see that the projectile reaches a height of 1,397.5 feet at 9.317 seconds (neglecting air resistance). This illustrates the convenience of using variables. The MATLAB code reads much like our original equations did. | ||
| + | |||
| + | === Tips on Defining Variables === | ||
| + | * Variables in MATLAB are ''case-sensitive''. That means that <tt>myVariable</tt>, <tt>myvariable</tt>, <tt>MyVariable</tt> and <tt>MYVARIABLE</tt> are all ''different'' variables and can all have different values. | ||
| + | * Variables may be defined by other variables. In that case, the righ-hand side is evaluated and then stored in the variable. For example: | ||
| + | <source lang="matlab"> | ||
| + | a=5; % a is 1. | ||
| + | b = a+2; % b is 7. | ||
| + | a=1; % b is still 7, a is 1. | ||
| + | </source> | ||
| + | * Variables may hold numbers or strings (characters). For example: | ||
| + | <source lang="matlab"> | ||
| + | a=pi; % a is 3.14159265... | ||
| + | a = "hello"; % a is now "hello" | ||
| + | </source> | ||
| + | * Use a semicolon ''';''' to terminate every MATLAB statement. Omitting the semicolon will result in the results being displayed in the command window. This is not good practice in general. | ||
| + | ** To print out variables, use the [[Matlab_IO|Input/Output]] techniques provided by MATLAB. | ||
| + | * See [[Matlab_Arrays|this link]] for information on defining arrays (vectors & matrices). | ||
| + | |||
| + | '''The following should NOT be used in variable names:''' | ||
| + | * Special characters like <tt>- + = / * & ^ % $ # @ ! [ ] ( ) : ' " .</tt> | ||
| + | * Spaces. For example <tt>my variable</tt> is NOT a valid variable name. | ||
| + | * Do not start a variable name with a number. Example: <tt>2a</tt> is not a valid variable name, but <tt>a2</tt> is. | ||
| + | |||
| + | == Basic Commands & Operations == | ||
=== Useful Commands === | === Useful Commands === | ||
| + | |||
| + | Often we want to see what variables we have defined in the MATLAB workspace. Or we may want to clear a variable. The commands in the following table illustrate several useful tools for managing variables. | ||
{| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| Line 52: | Line 117: | ||
clear; | clear; | ||
a=5; b=6; c=a+b*2; | a=5; b=6; c=a+b*2; | ||
| − | save myVariables; | + | save myVariables; % save all variables to a file |
| − | save bcVars b c; | + | save bcVars b c; % save b and c to a file |
| − | clear; | + | clear; % no variables defined. |
load bcVars; % b and c are now defined. | load bcVars; % b and c are now defined. | ||
who; | who; | ||
| − | clear; | + | clear; % no variables defined. |
load myVariables; % a b and c are all defined. | load myVariables; % a b and c are all defined. | ||
who; | who; | ||
| Line 71: | Line 136: | ||
|} | |} | ||
| − | |||
| − | MATLAB | + | |
| + | === Basic Operations & Common Functions === | ||
| + | |||
| + | In the [[Matlab_Basics#Example|projectile example]] above we saw examples of using several basic operators in MATLAB. The following table summarizes the basic operators and gives simple examples of their usage. | ||
{| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| Line 100: | Line 167: | ||
| <tt>*</tt> || Multiplication | | <tt>*</tt> || Multiplication | ||
|<source lang="matlab"> | |<source lang="matlab"> | ||
| − | 2.2*3.3 % displays | + | 2.2*3.3 % displays 7.26 |
| − | a = 2.2*3.3; % assigns | + | a = 2.2*3.3; % assigns 7.26 to a. |
| − | b = (pi/4); % assigns | + | b = (pi/4); % assigns pi/4 to b. |
</source> | </source> | ||
| Line 108: | Line 175: | ||
| <tt>/</tt> || Division | | <tt>/</tt> || Division | ||
|<source lang="matlab"> | |<source lang="matlab"> | ||
| − | + | 7.26/2.2 % dispays 3.3 | |
| − | a = | + | a = 7.26/2.2; % assigns 3.3 to a. |
b = sqrt(a/pi)*exp(a); | b = sqrt(a/pi)*exp(a); | ||
</source> | </source> | ||
| Line 145: | Line 212: | ||
| tan || The tangent function | | tan || The tangent function | ||
|- | |- | ||
| − | | sqrt || The square-root, <math>\sqrt | + | | sqrt || The square-root, <math>\sqrt{x}=x^{1/2}</math> |
|- | |- | ||
| exp || The exponential function | | exp || The exponential function | ||
|- | |- | ||
| − | | log10 || The base-10 log function, <math>\log(10^x)=x</math> | + | | log10 || The '''base-10 log''' function, <math>\log(10^x)=x</math> |
|- | |- | ||
| − | | log || The natural log function, <math>\ln(\exp(x))=x</math> | + | | log || The '''natural log''' function, <math>\ln(\exp(x))=x</math> |
|- | |- | ||
| abs || The absolute value, <math>\left|x\right|</math> | | abs || The absolute value, <math>\left|x\right|</math> | ||
|} | |} | ||
| + | == M-Files == | ||
| + | An M-file is a series of MATLAB commands that you save in a file. Then you can re-run them easily and make changes without re-entering everything again. Anything that can be done in the command window can also be done from an m-file. As an example, let's reconsider the [[#Defining_Variables|projectile example]] discussed earlier. We had the following MATLAB commands that we entered in the command window: | ||
| + | <source lang="matlab"> | ||
| + | y0 = 0.0; % initial height (feet) | ||
| + | v0 = 300; % initial velocity (feet/s) | ||
| + | vt = 0.0; % final velocity (feet/s) | ||
| + | a = -32.2; % gravitational acceleration (feet^2/s) | ||
| + | t = (vt-v0)/a; % time (s) when the bullet stops (maximum height) | ||
| + | yt = y0 + v0*t + a*t^2/2; % maximum height (feet). | ||
| + | </source> | ||
| − | == M-Files == | + | Suppose that we wanted to change the initial velocity. We could re-enter everything again, ''or'' we could save these commands in a m-file. To use an m-file, follow these steps: |
| − | {{ | + | # Choose <tt>File→New→M-File</tt>. |
| + | # Enter the MATLAB commands just as you would in the command window and save the file. You may save it wherever you wish. | ||
| + | # Navigate to the directory where you saved the file. Do this one of two ways: [[image:matlabCmdWindow_arrows.jpg|right]] | ||
| + | #* Type the directory in the location box in the top of the MATLAB command window (the current directory). | ||
| + | #* Select the button to navigate to the directory where your m-file is saved. | ||
| + | # Now you can type the name of your m-file in the command window to run it. For example, if I named the file <tt>projectile.m</tt>, I would type <source lang="matlab">projectile</source> at the command prompt. MATLAB will then execute all of the statements in the m-file as if you had entered them into the command window (although they will not be shown in the command window). | ||
| + | |||
| + | Step 3 may be ommitted if the directory is already set in [[#Matlab's_Path|Matlab's path]], as discussed in the following section. | ||
| + | <br clear="all" /> | ||
| + | |||
| + | === Naming M-Files === | ||
| + | |||
| + | When choosing a name for your file, keep the following guidelines in mind: | ||
| + | * Do not use spaces in the name. You may use an underscore "_" in lieu of a space. | ||
| + | * Do not use any symbols in the name: Examples of things NOT to put in the name: / + = - ^ * ! # % @ ( ) & . Using these symbols confuses MATLAB. | ||
| + | * Do not begin your file name with a number. You may have numbers elsewhere in your file. | ||
| + | |||
| + | The following table illustrates some valid and invalid file names. | ||
| + | {|border="1" cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | ! Valid File Names !! Invalid File Names | ||
| + | |- | ||
| + | | myFile.m || my File.m | ||
| + | |- | ||
| + | | problem5.m || 5prob.m | ||
| + | |- | ||
| + | | crazy_file.m || crazy-file.m | ||
| + | |} | ||
| + | |||
| + | === Documenting M-Files === | ||
| + | |||
| + | As you know by now, you can use Matlab's "<tt>help</tt>" command to get help on using various Matlab commands. However, you can document your own m-files so that you can get help on them as well. For example, consider the following code saved in a file called <tt>projectile.m</tt> | ||
| + | {| style="background-color:Beige; border: 2px solid #ccc" | ||
| + | |+ projectile.m | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | % This script calculates the maximum height of a projectile | ||
| + | % as a function of its initial height and vertical velocity. | ||
| + | y0 = 0.0; % initial height (feet) | ||
| + | v0 = 300; % initial velocity (feet/s) | ||
| + | vt = 0.0; % final velocity (feet/s) | ||
| + | a = -32.2; % gravitational acceleration (feet^2/s) | ||
| + | t = (vt-v0)/a; % time (s) when the bullet stops (maximum height) | ||
| + | yt = y0 + v0*t + a*t^2/2; % maximum height (feet). | ||
| + | disp('The maximum height (feet) is:'); | ||
| + | disp(yt); | ||
| + | disp('This occurs at time (seconds):'); | ||
| + | disp(t); | ||
| + | </source> | ||
| + | |} | ||
| + | |||
| + | Typing <tt>help projectile</tt> in the command window will result in the following: | ||
| + | |||
| + | :<tt>This script calculates the maximum height of a projectile</tt> | ||
| + | :<tt>as a function of its initial height and vertical velocity.</tt> | ||
| + | |||
| + | == Matlab's Path == | ||
| + | |||
| + | ; path : A list of directories that MATLAB looks in to find m-files. | ||
| + | |||
| + | When you type a command in the MATLAB command window, MATLAB decides what to do based on the following: | ||
| + | # Look to see if a variable by that name exists. If so, use it. | ||
| + | # If no variables match, then MATLAB looks in the current directory to see if there are any m-files that match the command name. | ||
| + | # If no m-files match in the current directory, then MATLAB looks through all directories in its ''path'' to see if there is an m-file in those directories whose name matches the command. | ||
| + | |||
| + | [[image:matlabPathDialogue.jpg|right]] | ||
| + | If no variables and no m-files match the command, then MATLAB issues an error message. | ||
| − | + | To set MATLAB's path, go to <tt>File→Set Path</tt>. You will see an image similar to the one at the right. Choose the <tt>Add Folder</tt> button and navigate to a folder containing m-files that you want to add to MATLAB's path. Then click <tt>Save</tt>. Now you don't have to have MATLAB running in the same directory where you saved your m-file. | |
| − | = | + | <br clear="all" /> |
| − | |||
Latest revision as of 14:34, 23 December 2010
Contents
The Command Window
MATLAB's command window can be used as a very powerful calculator. The >> indicates that MATLAB is ready to accept a command. It works much like your calculator. For example,
>> 1 + cos(pi/2)
ans =
1
>> 5^2 % square 5
ans =
25
Note that anything following a % on a line is ignored. This allows us to include comments in our calculations.
Defining Variables
By using variables instead of numbers, our calculations look much like they would on paper. For example, from physics we know that projectile motion (in the absence of air resistance) is governed by the equations
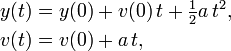
where 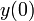 and
and 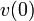 are the position and velocity of the projectile at time
are the position and velocity of the projectile at time 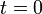 and
and 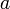 is the acceleration.
is the acceleration.
Example
Assume that we have the following problem:
A bullet is shot upward with an initial velocity of 300 feet per second (fps). Neglecting air resistance, determine the maximum height of the bullet.
The maximum height occurs when 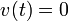 . We can solve the equation for
. We can solve the equation for 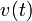 to find
to find
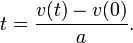
This gives the time at which the bullet reaches its maximum height. We can then use the equation for 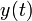 to determine how high it is at that time.
to determine how high it is at that time.
Let's solve this in MATLAB. First we define the initial height, the initial velocity, and the acceleration. We also know the final velocity - it is zero.
y0 = 0.0; % initial height (feet)
v0 = 300; % initial velocity (feet/s)
vt = 0.0; % final velocity (feet/s)
a = -32.2; % gravitational acceleration (feet^2/s)
Now we can define the time that the projectile reaches its maximum height, and then determine what the maximum height is. We use the variables we just defined:
t = (vt-v0)/a; % time (s) when the bullet stops (maximum height)
yt = y0 + v0*t + a*t^2/2; % maximum height (feet).
If we omit the ; on the line for yt MATLAB will print its value. Or we can simply type the variable and MATLAB will print it. Doing this we see that the projectile reaches a height of 1,397.5 feet at 9.317 seconds (neglecting air resistance). This illustrates the convenience of using variables. The MATLAB code reads much like our original equations did.
Tips on Defining Variables
- Variables in MATLAB are case-sensitive. That means that myVariable, myvariable, MyVariable and MYVARIABLE are all different variables and can all have different values.
- Variables may be defined by other variables. In that case, the righ-hand side is evaluated and then stored in the variable. For example:
a=5; % a is 1.
b = a+2; % b is 7.
a=1; % b is still 7, a is 1.
- Variables may hold numbers or strings (characters). For example:
a=pi; % a is 3.14159265...
a = "hello"; % a is now "hello"
- Use a semicolon ; to terminate every MATLAB statement. Omitting the semicolon will result in the results being displayed in the command window. This is not good practice in general.
- To print out variables, use the Input/Output techniques provided by MATLAB.
- See this link for information on defining arrays (vectors & matrices).
The following should NOT be used in variable names:
- Special characters like - + = / * & ^ % $ # @ ! [ ] ( ) : ' " .
- Spaces. For example my variable is NOT a valid variable name.
- Do not start a variable name with a number. Example: 2a is not a valid variable name, but a2 is.
Basic Commands & Operations
Useful Commands
Often we want to see what variables we have defined in the MATLAB workspace. Or we may want to clear a variable. The commands in the following table illustrate several useful tools for managing variables.
| Command | Description | Example (try these out) |
|---|---|---|
| who | Lists variables currently defined in MATLAB. | a = 5; b = 6; c = linspace(0,50,10);
who
|
| whos | Similar to who, but gives additional information. | a = 5; b = 6; c = linspace(0,50,10);
whos
|
| clear | Clear all variables defined. | a = 5; b = 6; c = linspace(0,50,10);
clear; % clears all variables
who; % displays nothing - no variables defined.
a=2; b=5; c=a+b;
clear a b; % only clears a and b. c is still here.
who; % tells us that c is defined.
|
| clc | Clears the MATLAB workspace. Doesn't clear variables | clc
|
| save | saves variables to a file that can be loaded later. | clear;
a=5; b=6; c=a+b*2;
save myVariables; % saves all variables to the file "myVariables.mat"
save bcVars b c; % saves b and c only to "bcVars.mat"
|
| load | loads variables from a file | clear;
a=5; b=6; c=a+b*2;
save myVariables; % save all variables to a file
save bcVars b c; % save b and c to a file
clear; % no variables defined.
load bcVars; % b and c are now defined.
who;
clear; % no variables defined.
load myVariables; % a b and c are all defined.
who;
|
| help | provides help on how to use a command | help clear;
help load;
help save;
|
Basic Operations & Common Functions
In the projectile example above we saw examples of using several basic operators in MATLAB. The following table summarizes the basic operators and gives simple examples of their usage.
| Operator | Description | Examples |
|---|---|---|
| + | Addition | 1 + 2 % displays 3
b = 1+2; % assigns 3 to the variable b.
a = cos(pi)+2.0; % a=1
|
| - | Subtraction | 1 - 2 % displays -1
b = 1-2; % assigns -1 to the variable b.
a = sqrt(-4*b)+2.0; % a=4
|
| * | Multiplication | 2.2*3.3 % displays 7.26
a = 2.2*3.3; % assigns 7.26 to a.
b = (pi/4); % assigns pi/4 to b.
|
| / | Division | 7.26/2.2 % dispays 3.3
a = 7.26/2.2; % assigns 3.3 to a.
b = sqrt(a/pi)*exp(a);
|
| ^ | Power | 2^3 % displays 8
a = 2^3 + 243^0.2; % assigns 11 to a.
|
| ( ) | Parentheses | a = (2+5)*3; % assigns 21 to a
b = 2+5*3; % assigns 17 to b
c = 2*(a-10); % assigns 22 to c
|
NOTE: if you are using arrays, then the / and * operators have different behavior! See the page on array arithmetic for more information.
In addition, MATLAB has many built-in functions. Type help elfun at the MATLAB command prompt for a list. Some commonly used functions are given here:
| Function | Description |
|---|---|
| cos | The cosine function |
| sin | The sine function |
| tan | The tangent function |
| sqrt | The square-root, 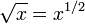
|
| exp | The exponential function |
| log10 | The base-10 log function, 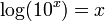
|
| log | The natural log function, 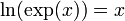
|
| abs | The absolute value, 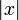
|
M-Files
An M-file is a series of MATLAB commands that you save in a file. Then you can re-run them easily and make changes without re-entering everything again. Anything that can be done in the command window can also be done from an m-file. As an example, let's reconsider the projectile example discussed earlier. We had the following MATLAB commands that we entered in the command window:
y0 = 0.0; % initial height (feet)
v0 = 300; % initial velocity (feet/s)
vt = 0.0; % final velocity (feet/s)
a = -32.2; % gravitational acceleration (feet^2/s)
t = (vt-v0)/a; % time (s) when the bullet stops (maximum height)
yt = y0 + v0*t + a*t^2/2; % maximum height (feet).
Suppose that we wanted to change the initial velocity. We could re-enter everything again, or we could save these commands in a m-file. To use an m-file, follow these steps:
- Choose File→New→M-File.
- Enter the MATLAB commands just as you would in the command window and save the file. You may save it wherever you wish.
- Navigate to the directory where you saved the file. Do this one of two ways: Error creating thumbnail: Unable to save thumbnail to destination
- Type the directory in the location box in the top of the MATLAB command window (the current directory).
- Select the button to navigate to the directory where your m-file is saved.
- Now you can type the name of your m-file in the command window to run it. For example, if I named the file projectile.m, I would type at the command prompt. MATLAB will then execute all of the statements in the m-file as if you had entered them into the command window (although they will not be shown in the command window).
projectile
Step 3 may be ommitted if the directory is already set in Matlab's path, as discussed in the following section.
Naming M-Files
When choosing a name for your file, keep the following guidelines in mind:
- Do not use spaces in the name. You may use an underscore "_" in lieu of a space.
- Do not use any symbols in the name: Examples of things NOT to put in the name: / + = - ^ * ! # % @ ( ) & . Using these symbols confuses MATLAB.
- Do not begin your file name with a number. You may have numbers elsewhere in your file.
The following table illustrates some valid and invalid file names.
| Valid File Names | Invalid File Names |
|---|---|
| myFile.m | my File.m |
| problem5.m | 5prob.m |
| crazy_file.m | crazy-file.m |
Documenting M-Files
As you know by now, you can use Matlab's "help" command to get help on using various Matlab commands. However, you can document your own m-files so that you can get help on them as well. For example, consider the following code saved in a file called projectile.m
% This script calculates the maximum height of a projectile
% as a function of its initial height and vertical velocity.
y0 = 0.0; % initial height (feet)
v0 = 300; % initial velocity (feet/s)
vt = 0.0; % final velocity (feet/s)
a = -32.2; % gravitational acceleration (feet^2/s)
t = (vt-v0)/a; % time (s) when the bullet stops (maximum height)
yt = y0 + v0*t + a*t^2/2; % maximum height (feet).
disp('The maximum height (feet) is:');
disp(yt);
disp('This occurs at time (seconds):');
disp(t);
|
Typing help projectile in the command window will result in the following:
- This script calculates the maximum height of a projectile
- as a function of its initial height and vertical velocity.
Matlab's Path
- path
- A list of directories that MATLAB looks in to find m-files.
When you type a command in the MATLAB command window, MATLAB decides what to do based on the following:
- Look to see if a variable by that name exists. If so, use it.
- If no variables match, then MATLAB looks in the current directory to see if there are any m-files that match the command name.
- If no m-files match in the current directory, then MATLAB looks through all directories in its path to see if there is an m-file in those directories whose name matches the command.
If no variables and no m-files match the command, then MATLAB issues an error message.
To set MATLAB's path, go to File→Set Path. You will see an image similar to the one at the right. Choose the Add Folder button and navigate to a folder containing m-files that you want to add to MATLAB's path. Then click Save. Now you don't have to have MATLAB running in the same directory where you saved your m-file.