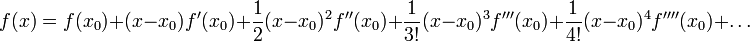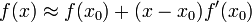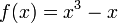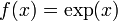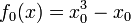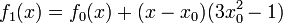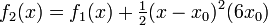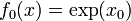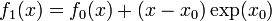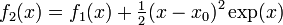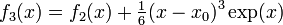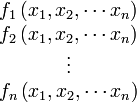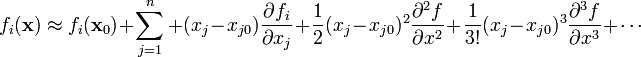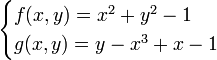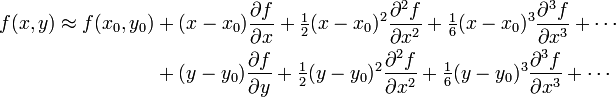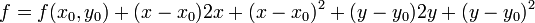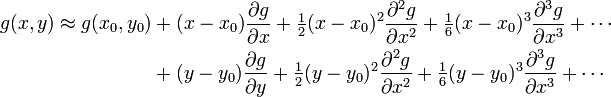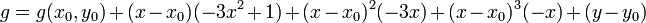Difference between revisions of "Taylor Series"
(→Single Variable Taylor Series: - fix mistake in table) |
(→Single Variable Taylor Series: - fix another mistake in table) |
||
| Line 42: | Line 42: | ||
* <math>f_0(x) = \exp(x_0)</math> | * <math>f_0(x) = \exp(x_0)</math> | ||
* <math>f_1(x) = f_0(x) + (x-x_0)\exp(x_0)</math> | * <math>f_1(x) = f_0(x) + (x-x_0)\exp(x_0)</math> | ||
| − | * <math>f_2(x) = f_1(x) + \tfrac{1}{2}(x-x_0)\exp(x)</math> | + | * <math>f_2(x) = f_1(x) + \tfrac{1}{2}(x-x_0)^2\exp(x)</math> |
| − | * <math>f_3(x) = f_2(x) + \tfrac{1}{6}(x-x_0)\exp(x)</math> | + | * <math>f_3(x) = f_2(x) + \tfrac{1}{6}(x-x_0)^3\exp(x)</math> |
Note that as we retain more terms we become increasingly more | Note that as we retain more terms we become increasingly more | ||
accurate. However, this is an infinite series for the exponential | accurate. However, this is an infinite series for the exponential | ||
Latest revision as of 19:19, 5 August 2009
Single Variable Taylor Series
If we know a function value and its derivatives at some point x0, we can use a Taylor series to approximate its value at a nearb point x as
If x-x0 is small then we can truncate the series to find
Note that for an nth order polynomial functions, the Taylor series converges in exactly n+1 terms.
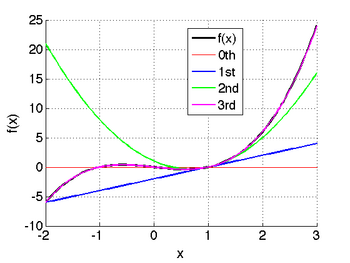
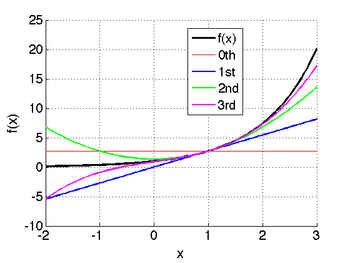
Taylor series approximation of various functions showing the effect of retaining up to 4 terms in the expansion. The expansions are: Note that the third expansion,
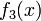 recovers the
function exactly at all points since all higher derivatives (and
therefore all higher terms in the expansion) are zero.
recovers the
function exactly at all points since all higher derivatives (and
therefore all higher terms in the expansion) are zero.
The expansions are: Note that as we retain more terms we become increasingly more accurate. However, this is an infinite series for the exponential function since all of its derivatives are nonzero.
-
Multivariate Taylor Series
Consider the case where we have several equations that are functions of multiple variables,
We can write a multivariate Taylor series expansion for the
ith function 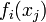 as
as
where 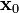 is the location where we evaluate the function and
is the location where we evaluate the function and 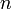 is the number of independent variables.
is the number of independent variables.
The term 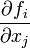 is a
matrix called the Jacobian matrix,
is a
matrix called the Jacobian matrix, ![[\mathbf{J}]](/wiki/images/math/0/a/d/0ad2c2c44fbd9ec9282f5b1769a30c70.png) It
is used in solving nonlinear systems of equations using
Newton's method.
It
is used in solving nonlinear systems of equations using
Newton's method.
Example
Consider the equations
Here  . Let's first look at the expansion for
. Let's first look at the expansion for 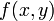 . Applying our general equation above we find
. Applying our general equation above we find
The partial derivatives of 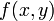 are:
are:
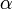
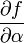
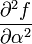
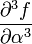
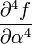
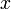
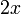
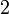
0 0 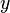
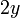
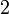
0 0
substituting this we find
We can do the same thing for 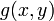
The partial derivatives of 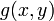 are:
are:
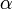
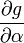
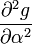
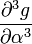
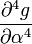
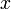
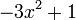
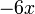
-6 0 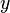
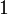
0 0 0
substituting this we find