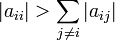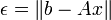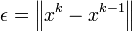Difference between revisions of "Linear Algebra"
m |
m (→Matrix-Matrix Product) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 71: | Line 71: | ||
* At noon, when the sun is directly overhead, a rocket is launched directly toward the sun at 1000 mph. How fast is its shadow moving? | * At noon, when the sun is directly overhead, a rocket is launched directly toward the sun at 1000 mph. How fast is its shadow moving? | ||
| − | + | *# Define the rocket's velocity as <math>\vec{R}</math>. | |
| − | + | *# Define the unit normal on the ground (i.e. the direction of the rocket's shadow on the ground) as <math>\vec{s}</math>, where <math>|\vec{s}| = 1</math>. | |
| − | : Intuition tells us that if the | + | *# The dot product between <math>\vec{R}</math> and <math>\vec{s}</math> gives us the component of the velocity in the direction of <math>\vec{s}</math>. Thus, the speed of the shadow along the ground is given by |
| + | *#: <math>v = \vec{R}\cdot\vec{s} = |\vec{R}|\,|\vec{s}| \cos(\theta)</math> | ||
| + | *# Intuition tells us that if the rocket is moving directly toward the sun, then its shadow does not appear to move at all. In this case, the angle between <math>\vec{R}</math> and <math>\vec{s}</math> is 90° and the dot product <math>\vec{R}\cdot\vec{s} = |\vec{R}| \, |\vec{s}| \cos(\theta) = 0</math> since <math>\cos(90^\circ)=0</math>. | ||
* Consider the same rocket going parallel to the earth's surface. How fast is its shadow moving? | * Consider the same rocket going parallel to the earth's surface. How fast is its shadow moving? | ||
| − | : If the rocket is going parallel to the earth's surface, our intuition tells us that is shadow is moving at the same speed. This is confirmed by the mathematics, since the angle between the rocket's path and the ground is 0. Therefore, <math>\vec{R}\cdot\vec{s} = |\vec{R}| \, |\vec{s}| \cos(\theta) = | + | : If the rocket is going parallel to the earth's surface, our intuition tells us that is shadow is moving at the same speed. This is confirmed by the mathematics, since the angle between the rocket's path and the ground is 0. Therefore, <math>\vec{R}\cdot\vec{s} = |\vec{R}| \, |\vec{s}| \cos(\theta) = |\vec{R}| \, |\vec{s}| = |\vec{R}|</math> since <math>\cos(0^\circ)=1</math> and <math>|\vec{s}|=1</math>. |
* What if the rocket were going at a 45° angle? | * What if the rocket were going at a 45° angle? | ||
: Our intuition tells us that the shadow will appear to move, but it will not be moving as fast as the rocket is moving. Mathematically, we have <math>v_s = \vec{R}\cdot\vec{s} = |\vec{R}| |\vec{s}| \cos(45^\circ) = 500\sqrt{2} = 707.1 \, \textrm{mph}</math>. | : Our intuition tells us that the shadow will appear to move, but it will not be moving as fast as the rocket is moving. Mathematically, we have <math>v_s = \vec{R}\cdot\vec{s} = |\vec{R}| |\vec{s}| \cos(45^\circ) = 500\sqrt{2} = 707.1 \, \textrm{mph}</math>. | ||
| − | |||
=== Vector Cross Product === | === Vector Cross Product === | ||
| Line 176: | Line 177: | ||
c=\left(\begin{array}{c} 34 \\ 64 \end{array}\right). | c=\left(\begin{array}{c} 34 \\ 64 \end{array}\right). | ||
</math></center> | </math></center> | ||
| + | |||
| + | ==== Geometric Interpretation of Matrix-Vector Product ==== | ||
| + | Here is a great discussion of how [http://www.mathworks.com/moler/exm/chapters/matrices.pdf a matrix-vector product can be interpreted geometrically]. | ||
==== Matrix-Vector product in MATLAB ==== | ==== Matrix-Vector product in MATLAB ==== | ||
| Line 206: | Line 210: | ||
|- | |- | ||
| <math>\left[\begin{smallmatrix} 1 \\ 2 \end{smallmatrix}\right]</math> | | <math>\left[\begin{smallmatrix} 1 \\ 2 \end{smallmatrix}\right]</math> | ||
| + | ||<math>\left[\begin{smallmatrix} 5 & 8 \end{smallmatrix}\right]</math> | ||
| + | | style="color:green" | Yes | ||
| + | || | ||
| + | |- | ||
| + | | <math>\left[\begin{smallmatrix} 1 & 2 \end{smallmatrix}\right]</math> | ||
||<math>\left[\begin{smallmatrix} 5 & 8 \end{smallmatrix}\right]</math> | ||<math>\left[\begin{smallmatrix} 5 & 8 \end{smallmatrix}\right]</math> | ||
| style="color:red" | No | | style="color:red" | No | ||
| − | || Number of columns in A= | + | || Number of columns in A=2, number of rows in B = 1. Therefore these cannot be multiplied. |
|} | |} | ||
| Line 384: | Line 393: | ||
| − | == | + | This page discusses a few methods to solve linear systems of |
| − | {{ | + | equations, <math>Ax=b</math>. There are two categories of solution |
| − | === Direct Solvers === | + | methods for linear systems of equations: |
| − | ==== | + | [[#Direct_Solvers|direct solvers]] and |
| − | ==== The | + | [[#Iterative_Solvers|iterative solvers]]. These will be discussed |
| + | briefly below. | ||
| + | |||
| + | |||
| + | == Direct Solvers == | ||
| + | |||
| + | Direct solvers solve the linear system to within the numeric precision | ||
| + | of the computer. There are many different algorithms for direct | ||
| + | solution of linear systems, but we will only mention two: | ||
| + | [[#Gaussian_Elimination|Gaussian elimination]] and | ||
| + | [[#The_Thomas_Algorithm (Tridiagonal Systems)|the Thomas Algorithm]]. | ||
| + | |||
| + | |||
| + | === Gaussian Elimination === | ||
| + | |||
| + | Gaussian elimination is a methododical approach to solving linear | ||
| + | systems of equations. It is essentially what you would do if you were | ||
| + | to solve a system of equations "by hand" but is systematic so that it | ||
| + | can be implemented on the computer. | ||
| + | For information on the algorithm, see this | ||
| + | [http://en.wikipedia.org/wiki/Gaussian_elimination wikipedia article]. | ||
| + | |||
| + | === The Thomas Algorithm (Tridiagonal Systems) === | ||
| + | |||
| + | The Thomas Algorithm is used for solving tridiagonal systems of | ||
| + | equations, <math>Ax=b</math>. A tridiagonal matrix is one where the | ||
| + | only non-zero entries in the matrix are on the main diagonal and the | ||
| + | lower and upper diagonals. In general a tridiagonal matrix can be | ||
| + | written as | ||
| + | :<math>A = \left[\begin{array}{ccccc} | ||
| + | d_1 & u_1 & 0 & \cdots & 0 \\ | ||
| + | \ell_1 & d_2 & u_2 & 0 & \cdots \\ | ||
| + | & \ddots & \ddots & \ddots & \\ | ||
| + | 0 & 0 & \cdots & \ell_{n-1} & d_n | ||
| + | \end{array}\right] | ||
| + | </math> | ||
| + | |||
| + | Here <math>d_i</math> represents the diagonal of the matrix, | ||
| + | <math>\ell_i</math> represents the lower-diagonal, and | ||
| + | <math>u_i</math> represents the upper-diagonal. | ||
| + | |||
| + | In terms of this nomenclature, the Thomas Algorithm can be written as | ||
| + | <code> | ||
| + | ''forward pass...'' | ||
| + | '''for''' i = 2 ... n | ||
| + | d(i) = d(i) - ( u(i-1)*ell(i-1) ) / d(i-1) | ||
| + | b(i) = b(i) - ( b(i-1)*ell(i-1) ) / d(i-1) | ||
| + | '''end''' | ||
| + | x(n) = b(n) / d(n) | ||
| + | ''backward pass...'' | ||
| + | '''for''' i = n-1 ... 1 | ||
| + | x(i) = ( b(i) - u(i) * x(i+1) ) / d(i) | ||
| + | '''end''' | ||
| + | </code> | ||
| + | |||
| + | == Iterative Solvers == | ||
| + | |||
| + | Iterative solvers are fundamentally different than | ||
| + | [[#Direct Solvers|direct solvers]]. They require an initial guess and | ||
| + | then refine the solution until a tolerance is reached. | ||
| + | |||
| + | |||
| + | === Jacobi Method === | ||
| + | |||
| + | The Jacobi method for solving linear systems is the simplest iterative | ||
| + | method. In this case, each iteration of the solution involves cycling | ||
| + | through the equations and solving the <var>i<sup>th</sup></var> | ||
| + | equation for the <var>x<sub>i</sub></var>, using values for all other | ||
| + | <var>x<sub>j</sub></var> from the previous iteration. | ||
| + | |||
| + | The algorithm for the Jacobi method is: | ||
| + | :<code> | ||
| + | xnew = x; | ||
| + | err = tol+1; | ||
| + | '''while''' err > tol | ||
| + | '''for''' i=1:1:n | ||
| + | ''update the i<sup>th</sup> value of x.'' | ||
| + | tmp = 0 | ||
| + | '''for''' j=1:1:i-1 | ||
| + | tmp = tmp + A(i,j) * x(j) | ||
| + | '''end''' | ||
| + | '''for''' j=i+1:1:n | ||
| + | tmp = tmp + A(i,j) * x(j) | ||
| + | '''end''' | ||
| + | xnew(i) = x(i) + ( b(j) - tmp ) / A(i,i) | ||
| + | '''end''' | ||
| + | x = xnew | ||
| + | ''check for convergence - set'' '''err''' | ||
| + | '''end''' | ||
| + | </code> | ||
| + | |||
| + | <span id="linsys_example"> <!-- anchor for linking --> | ||
| + | For example, assume that we have the following system of equations: | ||
| + | :<math> | ||
| + | \left[ \begin{array}{rrrr} | ||
| + | -3 & 1 & 0 & 0 \\ | ||
| + | 1 & -2 & 1 & 0 \\ | ||
| + | 0 & 1 & -2 & 1 \\ | ||
| + | 0 & 0 & 1 & -3 | ||
| + | \end{array} \right] | ||
| + | \left( \begin{array}{c} | ||
| + | x_1 \\ x_2 \\ x_3 \\ x_4 | ||
| + | \end{array} \right) | ||
| + | = | ||
| + | \left( \begin{array}{r} | ||
| + | -4 \\ 2 \\ 9 \\ 2 | ||
| + | \end{array} \right) | ||
| + | </math> | ||
| + | |||
| + | If we set our initial guess as <math>x=\left[ \begin{array}{cccc} 1 & 1 & | ||
| + | 1 & 1 \end{array} \right]^T</math> then for the first iteration we | ||
| + | proceed as follows: | ||
| + | |||
| + | * Solve the first equation for <var>x<sub>1</sub></var> to find <math> x_1 = \frac{-4 -x_2}{-3} = 5/3.</math> | ||
| + | |||
| + | * Solve the second equation for <var>x<sub>2</sub></var> to find <math> x_2 = \frac{2 - x_1-x_3}{-2} = 0.</math> | ||
| + | |||
| + | We repeat this for all of the equations. At the end of the first | ||
| + | iteration, we have | ||
| + | <math>x=\left(\begin{array}{cccc} 5/3, & 0, & -7/2, & -1/3 \end{array}\right).</math> | ||
| + | |||
| + | We are now ready to start with the second iteration, where we use the | ||
| + | newly computed values for <math>x_i</math>. The | ||
| + | [[#convergencetable|table below]] shows the results for the first few | ||
| + | iterations. | ||
| + | |||
| + | The last entry in the table is the analytic solution to this system of | ||
| + | equations. Note that after 40 iterations we have converged to the | ||
| + | exact answer to within an absolute error <var>x-x<sub>exact</sub> = | ||
| + | 10<sup>-3</sup></var>. | ||
| + | |||
| + | See [[media:jacobi.m|here]] for a Matlab implementation of the Jacobi | ||
| + | method. More information can be found | ||
| + | [http://en.wikipedia.org/wiki/Jacobi_method here]. | ||
| + | |||
| + | |||
| + | === Gauss-Seidel Method === | ||
| + | |||
| + | The Gauss-Seidel method is a simple extension of the Jacobi method. | ||
| + | The only difference is that rather than using "old" solution values, | ||
| + | we use the most up-to-date solution values in our calculation. | ||
| + | |||
| + | The algorithm for the Gauss-Seidel method is: | ||
| + | :<code> | ||
| + | err = tol+1 | ||
| + | '''while''' err > tol | ||
| + | '''for''' i=1:1:n | ||
| + | ''update x<sub>i</sub> with latest information on all other values of x'' | ||
| + | '''for''' j=1:1:n | ||
| + | tmp = tmp + A(i,j) * x(j) | ||
| + | '''end''' | ||
| + | x(i) = x(i) + ( b(i) - tmp ) / A(i,i) | ||
| + | '''end''' | ||
| + | ''check for convergence - set'' '''err''' | ||
| + | '''end''' | ||
| + | </code> | ||
| + | |||
| + | If we apply the Gauss-Seidel method to the | ||
| + | [[#linsys_example|example above]], we proceed as follows for the first | ||
| + | iteration: | ||
| + | |||
| + | * Solve the first equation for <var>x<sub>1</sub></var> to find <math>x_1 = \frac{-4 -x_2}{-3} = 5/3</math> | ||
| + | |||
| + | * Solve the second equation for <var>x<sub>2</sub></var> and use the most recent value of <var>x<sub>1</sub></var> to find <math>x_2 = \frac{2 - x_1-x_3)}{-2} = \frac{2-5/3-1}{-2} = 1/3</math> | ||
| + | |||
| + | We repeat this for all of the equations. At the end of the first | ||
| + | iteration, we have | ||
| + | <math>x=\left(\begin{array}{cccc} 5/3, & 1/3, & -23/6, & -35/18, \end{array}\right)</math> | ||
| + | |||
| + | The following table shows the convergence results for the Jacobi and | ||
| + | Gauss-Seidel methods. The Gauss-Seidel method converges much faster | ||
| + | than the Jacobi method. | ||
| + | |||
| + | <span id="convergencetable"> <!-- anchor for linking --> | ||
| + | |||
| + | :{| border="1" cellpadding="3" cellspacing="0" style="text=align:center" | ||
| + | |+ Convergence for the Jacobi and Gauss-Seidel iterative linear solvers | ||
| + | ! | ||
| + | ! style="text-align:center" colspan="4" | Jacobi Method | ||
| + | ! | ||
| + | ! style="text-align:center" colspan="4" | Gauss-Seidel Method | ||
| + | |- | ||
| + | | style="text-align:center" | Iteration | ||
| + | | <math>x_1</math> || <math>x_2</math> || <math>x_3</math> || <math>x_4</math> | ||
| + | | | ||
| + | | <math>x_1</math> || <math>x_2</math> || <math>x_3</math> || <math>x_4</math> | ||
| + | |- | ||
| + | ! 1 | ||
| + | | 5/3 || 0 || -7/2 || -1/3 | ||
| + | | | ||
| + | | 5/3 || 1/3 || -23/6 || -35/18 | ||
| + | |- | ||
| + | ! 2 | ||
| + | | 4/3 || -23/12 || -14/3 || -11/6 | ||
| + | | | ||
| + | | 1.4444 || -2.1944 || -6.5694 || -2.8565 | ||
| + | |- | ||
| + | ! 3 | ||
| + | | 25/26 || -8/3 || -51/8 || -20/9 | ||
| + | | | ||
| + | | 0.6019 || -3.9838 || -7.9201 || -3.3067 | ||
| + | |- | ||
| + | ! 4 | ||
| + | | 0.4444 || -3.8403 || -6.9444 || -2.7917 | ||
| + | | | ||
| + | | 0.0054 || -4.9574 || -8.6320 || -3.5440 | ||
| + | |- | ||
| + | ! 5 | ||
| + | | 0.0532 || -4.2500 || -7.8160 || -2.9815 | ||
| + | | | ||
| + | | -0.3191 || -5.4756 || -9.0098 || -3.6699 | ||
| + | |- | ||
| + | ! 10 | ||
| + | | -0.5170 || -5.7294 || -9.0648 || -3.6601 | ||
| + | | | ||
| + | | -0.6719 || -6.0377 || -9.4194 || -3.8065 | ||
| + | |- | ||
| + | ! 20 | ||
| + | | -0.6803 || -6.0484 || -9.4218 || -3.8061 | ||
| + | | | ||
| + | | -0.6875 || -6.0625 || -9.4375 || -3.8125 | ||
| + | |- | ||
| + | ! ∞ | ||
| + | | -11/16 = -0.6875 || -97/16 = -6.0625 || -151/16 = -9.4375 || -61/16 = -3.8125 | ||
| + | |} | ||
| + | |||
| + | More information on the Gauss-Seidel method can be found | ||
| + | [http://en.wikipedia.org/wiki/Gauss-Seidel#Convergence here]. | ||
| + | |||
| + | |||
| + | === Some Caveats === | ||
| + | |||
| + | A [[#Direct Solvers|direct solver]] will always find a solution if the | ||
| + | system is well-posed. However, iterative solvers are more fragile, and | ||
| + | will occasionally not converge. This is particularly true for the | ||
| + | Jacobi and Gauss-Seidel solvers discussed above. In fact, the matrices | ||
| + | must have special properties for these solvers to converge. | ||
| + | Specifically, they must be symmetric and positive-definite or | ||
| + | diagonally dominant. What this means in practice is that in a given | ||
| + | row of the matrix, the diagonal coefficient is larger than the sum of | ||
| + | the off-diagonal coefficients, | ||
| + | :<math>\left| a_{ii} \right| > \sum_{j\ne i} \left| a_{ij} \right|</math> | ||
| + | |||
| + | === Other Iterative Methods === | ||
| + | |||
| + | There are many other iterative solvers that are much more | ||
| + | sophisticated and robust. Among them are the | ||
| + | [http://en.wikipedia.org/wiki/Conjugate_gradient Conjugate-Gradient] | ||
| + | and [http://en.wikipedia.org/wiki/Gmres GMRES] methods. | ||
| + | |||
| + | |||
| + | === Convergence === | ||
| + | |||
| + | Iterative solvers require us to decide when to stop iterating. In | ||
| + | other words, we need to decide when the solution is ''converged''. We | ||
| + | do this by comparing an error measure to a tolerance. | ||
| + | |||
| + | There are a few common ways to determine convergence for a linear | ||
| + | system: | ||
| + | * <math>\epsilon = \left\Vert b-Ax \right\Vert</math> | ||
| + | * <math>\epsilon = \left\Vert x^{k}-x^{k-1}\right\Vert</math> | ||
| + | where the terms <math>\left\Vert a \right\Vert</math> indicate an | ||
| + | appropriate [[Iteration_and_Convergence#Vector_Norms|vector norm]]. | ||
| − | + | See the discussion on | |
| − | + | [[Iteration_and_Convergence|iteration and convergence]] for more | |
| − | + | information on this topic. | |
| − | |||
| − | |||
| − | |||
Latest revision as of 11:23, 26 August 2016
Contents
Basics
Let's first make some definitions:
- Vector
- A one-dimensional collection of numbers. Examples:
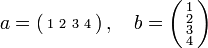
- Matrix
- A two-dimensional collection of numbers. Examples:
![A = \left[ \begin{smallmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{smallmatrix} \right], \quad B = \left[ \begin{smallmatrix} 9 & 6 \\ 2 & 3 \end{smallmatrix}\right]](/wiki/images/math/5/8/d/58df31b30651dbb7a29a51e1ba37f8ff.png)
- Array
- An n-dimensional collection of numbers. A vector is a 1-dimensional array while a matrix is a 2-dimensional array.
- Transpose
- An operation that involves interchanging the rows and columns of an array. It is indicated by a
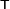 superscript. For example:
superscript. For example: 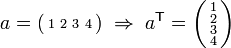 for a vector and
for a vector and ![A = \left[ \begin{smallmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{smallmatrix} \right] \; \Rightarrow \; A^\mathsf{T} = \left[ \begin{smallmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{smallmatrix} \right]](/wiki/images/math/a/2/7/a273e5ebba159e990d55fa9da022a691.png) for a matrix
for a matrix
- Vector Magnitude,

- A measure of the length of a vector,
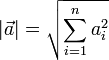
-
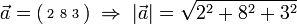
-
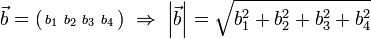
- Vector Norm,
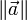
- A measure of the size of a vector
| Name | Definition |
|---|---|
| L1 norm | 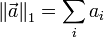
|
| L2 norm | 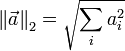
|
| L∞ norm | 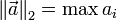
|
Matrix & Vector Algebra
There are many common operations involving matrices and vectors including:
These are each discussed in the following sub-sections.
Vector Dot Product
The dot product of two vectors produces a scalar. Physically, the dot product of a and b represents the projection of a onto b.
Given two vectors a and b, their dot product is formed as
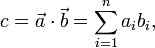
where 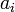 and
and 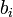 are the components in vectors a and b respectively. This is most useful when we know the components of the vectors a and b.
are the components in vectors a and b respectively. This is most useful when we know the components of the vectors a and b.
Occasionally we know the magnitude of the two vectors and the angle between them. In this case, we can calculate the dot product as
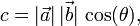
where θ is the angle between the vectors a and b.
Note that if a and b are both column vectors, then 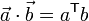 .
.
For more information on the dot product, see wikipedia's article.
Dot Product in MATLAB
There are several ways to calculate the dot product of two vectors in MATLAB:
c = dot(a,b);
c = a' * b; % if a and b are both column vectors.
Thought examples
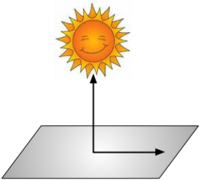
Consider the cartoon shown to the right.- At noon, when the sun is directly overhead, a rocket is launched directly toward the sun at 1000 mph. How fast is its shadow moving?
- Define the rocket's velocity as
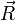 .
. - Define the unit normal on the ground (i.e. the direction of the rocket's shadow on the ground) as
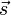 , where
, where 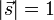 .
. - The dot product between
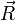 and
and 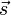 gives us the component of the velocity in the direction of
gives us the component of the velocity in the direction of 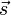 . Thus, the speed of the shadow along the ground is given by
. Thus, the speed of the shadow along the ground is given by
-
- Intuition tells us that if the rocket is moving directly toward the sun, then its shadow does not appear to move at all. In this case, the angle between
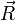 and
and 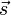 is 90° and the dot product
is 90° and the dot product 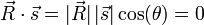 since
since 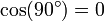 .
.
- Define the rocket's velocity as
- Consider the same rocket going parallel to the earth's surface. How fast is its shadow moving?
- If the rocket is going parallel to the earth's surface, our intuition tells us that is shadow is moving at the same speed. This is confirmed by the mathematics, since the angle between the rocket's path and the ground is 0. Therefore,
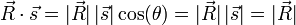 since
since 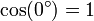 and
and 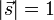 .
.
- What if the rocket were going at a 45° angle?
- Our intuition tells us that the shadow will appear to move, but it will not be moving as fast as the rocket is moving. Mathematically, we have
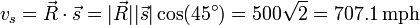 .
.
Vector Cross Product
The cross product of two vectors produces a vector perpendicular to the original two. The common right-hand rule is used to determine the direction of the resulting vector.
Assume that we have vectors a and b defined as
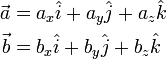
where 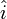 ,
, 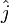 , and
, and 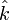 represent the unit-normal vectors in the x, y, and z directions, respectively.
The cross product of a and b is then defined as
represent the unit-normal vectors in the x, y, and z directions, respectively.
The cross product of a and b is then defined as
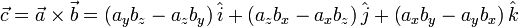
If we know the magnitude of a and b and the angle between them (θ), then the cross-product is given as
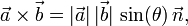
where n is the unit-normal vector perpendicular to the plane defined by the vectors a and b.
For more information, see wikipedia's article on the cross product.
Vector Cross Product in MATLAB
c = cross(a,b); % c is a vector!
Matrix-Vector Product
The matrix-vector product is frequently encountered in solving linear systems of equations, although there are many other uses for it.
Consider a matrix A with m rows and n columns and vector b with n rows:
![A=\left[\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \cdots & a_{mn}\end{array}\right],
\quad
b=
\left(\begin{array}{c}
b_{1}\\ b_{2}\\ \vdots\\ b_{n}
\end{array}\right)](/wiki/images/math/5/a/c/5ac41a50c2f681b1cb7b3641e692b7e0.png)
We may multiply A and b if the number of columns in A is equal to the number of rows in b. The product, c is a vector with m rows. The ith entry in c is given as
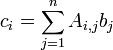
For example, let's consider the following case:
![A = \left[\begin{array}{ccc}
1 & 3 & 2 \\
2 & 5 & 4
\end{array}\right],
\quad
b = \left(\begin{array}{c}
10 \\ 4 \\ 6
\end{array} \right)](/wiki/images/math/0/9/a/09a75f9e23e7be0954f36ecd4d99a351.png)
Here we have m=2 and n=3. We define the product, c=Ab, as follows:
- Be sure that A and b are compatible for multiplication.
- Since A has three columns and b has three rows, they are compatible.
- Determine how many entries are in c.
- The c vector will have as many rows as A has.
- Since A has two rows, c will have two rows.
- Determine the elements in c
- Applying the above formula for i=1 we find
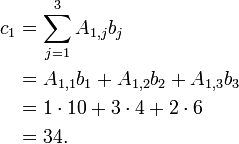
- Applying the above formula for i=2 we find
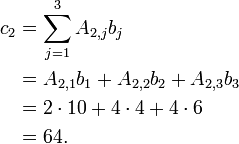
- Applying the above formula for i=1 we find
Therefore, we have
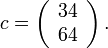
Geometric Interpretation of Matrix-Vector Product
Here is a great discussion of how a matrix-vector product can be interpreted geometrically.
Matrix-Vector product in MATLAB
c = A*b; % A is a matrix, b and c are vectors.
Matrix-Matrix Product
The matrix-matrix product is a generalization of the matrix-vector product. Consider the general case where we want to multiply two matrices, C = A B, where A and B are matrices. The following rules apply:
- The number of columns in A must be equal to the number of rows in B.
- The number of columns in C is equal to the number of columns in B.
- The number of rows in C is equal to the number of rows in A.
We can state this differently. Suppose that A has m rows and p columns, and that B has p rows and n columns. This satisfies rule 1 above. Then, according to rules 2 and 3, C has m rows and n columns.
| A | B | Valid? | Comments |
|---|---|---|---|
![\left[\begin{smallmatrix} 1 & 2 \\ 3 & 4 \end{smallmatrix}\right]](/wiki/images/math/8/b/1/8b1ed1378d351ba83fd0d18adf7b6f3a.png)
|
![\left[\begin{smallmatrix} 5 & 6 \\ 7 & 8 \end{smallmatrix}\right]](/wiki/images/math/5/b/0/5b072339bf884d51dfa9b0fd98445523.png)
|
Yes | Number of columns in A = 2, number or rows in B = 2. |
![\left[\begin{smallmatrix} 1 & 2 \end{smallmatrix}\right]](/wiki/images/math/5/6/a/56af0b427f425dbb0860f1a5aaa77ad9.png)
|
![\left[\begin{smallmatrix} 5 \\ 8 \end{smallmatrix}\right]](/wiki/images/math/4/b/7/4b7417f9359b8b278434293a4fd65578.png)
|
Yes | |
![\left[\begin{smallmatrix} 1 \\ 2 \end{smallmatrix}\right]](/wiki/images/math/1/d/7/1d7c1278b1791ebde17e8b2f8886f4da.png)
|
![\left[\begin{smallmatrix} 5 & 8 \end{smallmatrix}\right]](/wiki/images/math/8/7/9/8795022ce25fefa05082ba4a24c11385.png)
|
Yes | |
![\left[\begin{smallmatrix} 1 & 2 \end{smallmatrix}\right]](/wiki/images/math/5/6/a/56af0b427f425dbb0860f1a5aaa77ad9.png)
|
![\left[\begin{smallmatrix} 5 & 8 \end{smallmatrix}\right]](/wiki/images/math/8/7/9/8795022ce25fefa05082ba4a24c11385.png)
|
No | Number of columns in A=2, number of rows in B = 1. Therefore these cannot be multiplied. |
The general formula for matrix multiplication is
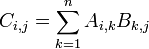
Let's show how this works for a simple example:
![A = \left[ \begin{array}{cc}
1 & 2 \\ 3 & 5
\end{array} \right],
\quad
B = \left[ \begin{array}{ccc}
2 & 4 & 10 \\ 6 & 3 & 1
\end{array} \right].](/wiki/images/math/a/3/3/a33807c3ad2ce2feda2960f4caecbe84.png)
We can form C=A B since rule 1 is satisfied. From the size of A and B we define m=2 and n=3 and from rules 2 and 3, we conclude that the resulting matrix, C has 2 rows and 3 columns.
We are now ready to build each element of C.
| Row | Column | Result |
|---|---|---|
| 1 | 1 | 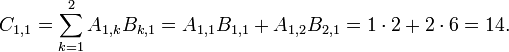
|
| 2 | 1 | 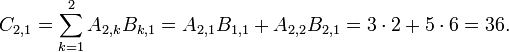
|
| 1 | 2 | 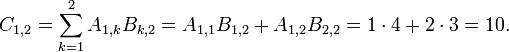
|
| 2 | 2 | 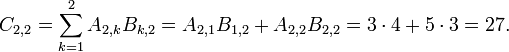
|
| 1 | 3 | 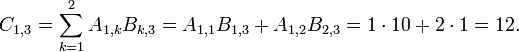
|
| 2 | 3 | 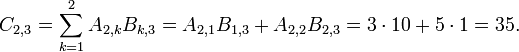
|
Now, putting all of these together, we have
![C=\left[\begin{array}{ccc}
14 & 10 & 12 \\
36 & 27 & 35
\end{array}\right].](/wiki/images/math/8/1/9/8197065e460efa184aa2ac872f7e37da.png)
Matrix-Matrix product in MATLAB
C = A*B; % A, B, and C are all matrices.
The MATLAB code to implement the above example is
A = [ 1 2; 3 5; ];
B = [ 2 4 10; 6 3 1; ];
C = A*B;
Linear Systems of Equations
Any set of linear systems may be written in the form =(b)](/wiki/images/math/b/3/a/b3ae30ff4dcdb54b97d86d814ca503d6.png) , where
, where ![[A]](/wiki/images/math/7/e/2/7e2bf8880d46cb84f91d8740b2659a88.png) is a matrix and
is a matrix and 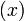 and
and 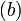 are vectors. In general, for a system of equations with n unknowns x1 ... xn, can be written as
are vectors. In general, for a system of equations with n unknowns x1 ... xn, can be written as
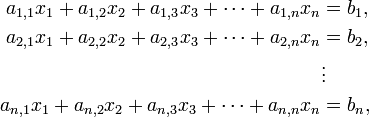
where 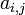 and
and 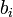 are numbers and
are numbers and 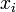 is the set of unknown variables. These equations can now be written in matrix format:
is the set of unknown variables. These equations can now be written in matrix format:
![\left[ \begin{array}{ccccc}
a_{1,1} & a_{1,2} & a_{1,3} & \cdots & a_{1,n} \\
a_{2,1} & a_{2,2} & a_{2,3} & \cdots & a_{2,n} \\
\vdots & \vdots & \ddots & \vdots & \vdots \\
a_{n,1} & a_{n,2} & a_{n,3} & \cdots & a_{n,n}
\end{array} \right]
\left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array} \right)
=
\left( \begin{array}{c} b_1 \\ b_2 \\ \vdots \\ b_n \end{array} \right).](/wiki/images/math/6/4/2/642696f07ee1eeb0986341fbd1b6e34a.png)
Example
Consider the following equations:
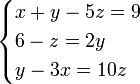
To put these in matrix format, we first choose the solution vector. Let's choose to order this as x, y, z. Now we rewrite the original system so that we have a coefficient multiplying each of these variables, and then we put the "constant" on the right-hand-side:
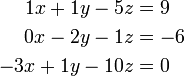
We may then identify the A matrix and b vectors and write
![\left[\begin{array}{ccc}
1 & 1 & -5 \\
0 & -2 & -1 \\
-3 & 1 & -10 \\
\end{array} \right]
\left( \begin{array}{c}
x \\ y \\ z
\end{array}\right)
=
\left( \begin{array}{c}
9 \\ -6 \\ 0
\end{array}\right)](/wiki/images/math/b/f/8/bf8e5ba530c6d522f80f30e36806149e.png)
Note that if we multiply the above matrix and vector, we recover the original set of equations (try it to be sure that you can do it).
Note that if we chose a different variable ordering, then it simply rearranges the columns in the matrix. For example, if we order the variables z, x, y then we have
![\begin{align}
-5z + 1x + 1y &= 9 \\
-1z + 0x - 2y &= -6 \\
-10z - 3x + 1y &= 0
\end{align}
\quad \Rightarrow \quad
\left[\begin{array}{ccc}
-5 & 1 & 1 \\
-1 & 0 & -2 \\
-10 & -3 & 1 \\
\end{array} \right]
\left( \begin{array}{c}
z \\ x \\ y
\end{array}\right)
=
\left( \begin{array}{c}
9 \\ -6 \\ 0
\end{array}\right)](/wiki/images/math/2/3/7/2371c4f3d9f6d52b195e09e4fba2cf55.png)
This page discusses a few methods to solve linear systems of
equations, 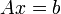 . There are two categories of solution
methods for linear systems of equations:
direct solvers and
iterative solvers. These will be discussed
briefly below.
. There are two categories of solution
methods for linear systems of equations:
direct solvers and
iterative solvers. These will be discussed
briefly below.
Direct Solvers
Direct solvers solve the linear system to within the numeric precision of the computer. There are many different algorithms for direct solution of linear systems, but we will only mention two: Gaussian elimination and the Thomas Algorithm.
Gaussian Elimination
Gaussian elimination is a methododical approach to solving linear systems of equations. It is essentially what you would do if you were to solve a system of equations "by hand" but is systematic so that it can be implemented on the computer. For information on the algorithm, see this wikipedia article.
The Thomas Algorithm (Tridiagonal Systems)
The Thomas Algorithm is used for solving tridiagonal systems of
equations, 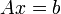 . A tridiagonal matrix is one where the
only non-zero entries in the matrix are on the main diagonal and the
lower and upper diagonals. In general a tridiagonal matrix can be
written as
. A tridiagonal matrix is one where the
only non-zero entries in the matrix are on the main diagonal and the
lower and upper diagonals. In general a tridiagonal matrix can be
written as
Here 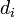 represents the diagonal of the matrix,
represents the diagonal of the matrix,
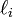 represents the lower-diagonal, and
represents the lower-diagonal, and
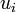 represents the upper-diagonal.
represents the upper-diagonal.
In terms of this nomenclature, the Thomas Algorithm can be written as
forward pass... for i = 2 ... n d(i) = d(i) - ( u(i-1)*ell(i-1) ) / d(i-1) b(i) = b(i) - ( b(i-1)*ell(i-1) ) / d(i-1) end x(n) = b(n) / d(n) backward pass... for i = n-1 ... 1 x(i) = ( b(i) - u(i) * x(i+1) ) / d(i) end
Iterative Solvers
Iterative solvers are fundamentally different than direct solvers. They require an initial guess and then refine the solution until a tolerance is reached.
Jacobi Method
The Jacobi method for solving linear systems is the simplest iterative method. In this case, each iteration of the solution involves cycling through the equations and solving the ith equation for the xi, using values for all other xj from the previous iteration.
The algorithm for the Jacobi method is:
xnew = x;
err = tol+1;
while err > tol
for i=1:1:n
update the ith value of x.
tmp = 0
for j=1:1:i-1
tmp = tmp + A(i,j) * x(j)
end
for j=i+1:1:n
tmp = tmp + A(i,j) * x(j)
end
xnew(i) = x(i) + ( b(j) - tmp ) / A(i,i)
end
x = xnew
check for convergence - set err
end
For example, assume that we have the following system of equations:
If we set our initial guess as ![x=\left[ \begin{array}{cccc} 1 & 1 &
1 & 1 \end{array} \right]^T](/wiki/images/math/7/7/c/77cc49e2b2e6356e6336b8b8c82f46c1.png) then for the first iteration we
proceed as follows:
then for the first iteration we
proceed as follows:
- Solve the first equation for x1 to find
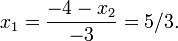
- Solve the second equation for x2 to find
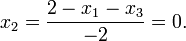
We repeat this for all of the equations. At the end of the first
iteration, we have
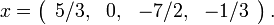
We are now ready to start with the second iteration, where we use the
newly computed values for 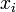 . The
table below shows the results for the first few
iterations.
. The
table below shows the results for the first few
iterations.
The last entry in the table is the analytic solution to this system of equations. Note that after 40 iterations we have converged to the exact answer to within an absolute error x-xexact = 10-3.
See here for a Matlab implementation of the Jacobi method. More information can be found here.
Gauss-Seidel Method
The Gauss-Seidel method is a simple extension of the Jacobi method. The only difference is that rather than using "old" solution values, we use the most up-to-date solution values in our calculation.
The algorithm for the Gauss-Seidel method is:
err = tol+1
while err > tol
for i=1:1:n
update xi with latest information on all other values of x
for j=1:1:n
tmp = tmp + A(i,j) * x(j)
end
x(i) = x(i) + ( b(i) - tmp ) / A(i,i)
end
check for convergence - set err
end
If we apply the Gauss-Seidel method to the example above, we proceed as follows for the first iteration:
- Solve the first equation for x1 to find
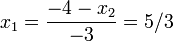
- Solve the second equation for x2 and use the most recent value of x1 to find
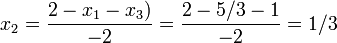
We repeat this for all of the equations. At the end of the first
iteration, we have
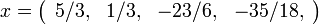
The following table shows the convergence results for the Jacobi and Gauss-Seidel methods. The Gauss-Seidel method converges much faster than the Jacobi method.
Convergence for the Jacobi and Gauss-Seidel iterative linear solvers Jacobi Method Gauss-Seidel Method Iteration 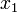
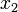
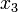
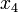
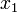
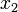
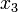
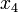
1 5/3 0 -7/2 -1/3 5/3 1/3 -23/6 -35/18 2 4/3 -23/12 -14/3 -11/6 1.4444 -2.1944 -6.5694 -2.8565 3 25/26 -8/3 -51/8 -20/9 0.6019 -3.9838 -7.9201 -3.3067 4 0.4444 -3.8403 -6.9444 -2.7917 0.0054 -4.9574 -8.6320 -3.5440 5 0.0532 -4.2500 -7.8160 -2.9815 -0.3191 -5.4756 -9.0098 -3.6699 10 -0.5170 -5.7294 -9.0648 -3.6601 -0.6719 -6.0377 -9.4194 -3.8065 20 -0.6803 -6.0484 -9.4218 -3.8061 -0.6875 -6.0625 -9.4375 -3.8125 ∞ -11/16 = -0.6875 -97/16 = -6.0625 -151/16 = -9.4375 -61/16 = -3.8125
More information on the Gauss-Seidel method can be found here.
Some Caveats
A direct solver will always find a solution if the system is well-posed. However, iterative solvers are more fragile, and will occasionally not converge. This is particularly true for the Jacobi and Gauss-Seidel solvers discussed above. In fact, the matrices must have special properties for these solvers to converge. Specifically, they must be symmetric and positive-definite or diagonally dominant. What this means in practice is that in a given row of the matrix, the diagonal coefficient is larger than the sum of the off-diagonal coefficients,
Other Iterative Methods
There are many other iterative solvers that are much more sophisticated and robust. Among them are the Conjugate-Gradient and GMRES methods.
Convergence
Iterative solvers require us to decide when to stop iterating. In other words, we need to decide when the solution is converged. We do this by comparing an error measure to a tolerance.
There are a few common ways to determine convergence for a linear system:
where the terms 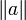 indicate an
appropriate vector norm.
indicate an
appropriate vector norm.
See the discussion on iteration and convergence for more information on this topic.
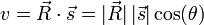
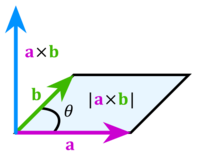
![A = \left[\begin{array}{ccccc}
d_1 & u_1 & 0 & \cdots & 0 \\
\ell_1 & d_2 & u_2 & 0 & \cdots \\
& \ddots & \ddots & \ddots & \\
0 & 0 & \cdots & \ell_{n-1} & d_n
\end{array}\right]](/wiki/images/math/a/4/e/a4eaff67fbb59c90bad068cc5f4a4ecd.png)
![\left[ \begin{array}{rrrr}
-3 & 1 & 0 & 0 \\
1 & -2 & 1 & 0 \\
0 & 1 & -2 & 1 \\
0 & 0 & 1 & -3
\end{array} \right]
\left( \begin{array}{c}
x_1 \\ x_2 \\ x_3 \\ x_4
\end{array} \right)
=
\left( \begin{array}{r}
-4 \\ 2 \\ 9 \\ 2
\end{array} \right)](/wiki/images/math/d/0/3/d0322246779d172c69c3da39c60f3657.png)