Difference between revisions of "Matlab Basics"
(→The Command Window) |
m (→Defining Variables) |
||
| Line 31: | Line 31: | ||
Let's solve this in MATLAB. First we define the initial height, the initial velocity, and the acceleration. We also know the final velocity - it is zero. | Let's solve this in MATLAB. First we define the initial height, the initial velocity, and the acceleration. We also know the final velocity - it is zero. | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| − | y0 = 0; | + | y0 = 0.0; % initial height (feet) |
v0 = 300; % initial velocity (feet/s) | v0 = 300; % initial velocity (feet/s) | ||
| − | vt = 0; | + | vt = 0.0; % final velocity (feet/s) |
a = -32.2; % gravitational acceleration (feet^2/s) | a = -32.2; % gravitational acceleration (feet^2/s) | ||
</source> | </source> | ||
Revision as of 10:17, 19 August 2008
Contents
The Command Window
MATLAB's command window can be used as a very powerful calculator. The >> indicates that MATLAB is ready to accept a command. It works much like your calculator. For example,
>> 1 + cos(pi/2)
ans =
1
>> 5^2 % square 5
ans =
25
Note that anything following a % on a line is ignored. This allows us to include comments in our calculations.
Defining Variables
By using variables instead of numbers, our calculations look much like they would on paper. For example, from physics we know that projectile motion (in the absence of air resistance) is governed by the equations
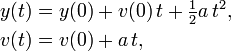
where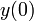 
and 
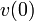are the position and velocity of the projectile at time 
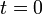and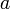 
is the acceleration.
Assume that we have the following problem:
A bullet is shot upward with an initial velocity of 300 feet per second (fps). Determine the maximum height of the bullet.
The maximum height occurs when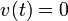 
. We can solve the equation for 
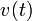to find
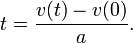
This gives the time at which the bullet reaches its maximum height. We can then use the equation for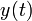 
to determine how high it is at that time.
Let's solve this in MATLAB. First we define the initial height, the initial velocity, and the acceleration. We also know the final velocity - it is zero.
y0 = 0.0; % initial height (feet)
v0 = 300; % initial velocity (feet/s)
vt = 0.0; % final velocity (feet/s)
a = -32.2; % gravitational acceleration (feet^2/s)
Now we can define the time that the projectile reaches its maximum height, and then determine what the maximum height is. We use the variables we just defined:
t = (vt-v0)/a; % time when the bullet stops (maximum height)
yt = y0 + v0*t + a*t^2/2; % maximum height.
If we omit the ; on the line for yt MATLAB will print its value. Or we can simply type the variable and MATLAB will print it. Doing this we see that the projectile reaches a height of 1,397.5 feet at 9.317 seconds (neglecting air resistance). This illustrates the convenience of using variables. The MATLAB code reads much like our original equations did.
Useful Commands
Often we want to see what variables we have defined in the MATLAB workspace. Or we may want to clear a variable. The commands in the following table illustrate several useful tools for managing variables.
| Command | Description | Example (try these out) |
|---|---|---|
| who | Lists variables currently defined in MATLAB. | a = 5; b = 6; c = linspace(0,50,10);
who
|
| whos | Similar to who, but gives additional information. | a = 5; b = 6; c = linspace(0,50,10);
whos
|
| clear | Clear all variables defined. | a = 5; b = 6; c = linspace(0,50,10);
clear; % clears all variables
who; % displays nothing - no variables defined.
a=2; b=5; c=a+b;
clear a b; % only clears a and b. c is still here.
who; % tells us that c is defined.
|
| clc | Clears the MATLAB workspace. Doesn't clear variables | clc
|
| save | saves variables to a file that can be loaded later. | clear;
a=5; b=6; c=a+b*2;
save myVariables; % saves all variables to the file "myVariables.mat"
save bcVars b c; % saves b and c only to "bcVars.mat"
|
| load | loads variables from a file | clear;
a=5; b=6; c=a+b*2;
save myVariables;
save bcVars b c;
clear;
load bcVars; % b and c are now defined.
who;
clear;
load myVariables; % a b and c are all defined.
who;
|
| help | provides help on how to use a command | help clear;
help load;
help save;
|
Basic Operations
MATLAB supports basic operations
| Operator | Description | Examples |
|---|---|---|
| + | Addition | 1 + 2 % displays 3
b = 1+2; % assigns 3 to the variable b.
a = cos(pi)+2.0; % a=1
|
| - | Subtraction | 1 - 2 % displays -1
b = 1-2; % assigns -1 to the variable b.
a = sqrt(-4*b)+2.0; % a=4
|
| * | Multiplication | 2.2*3.3 % displays 6.6
a = 2.2*3.3; % assigns 6.6 to a.
b = (pi/4); % assigns sqrt(2)/2 to b.
|
| / | Division | 6.6/2.2 % dispays 3.3
a = 6.6/2.2; % assigns 3.3 to a.
b = sqrt(a/pi)*exp(a);
|
| ^ | Power | 2^3 % displays 8
a = 2^3 + 243^0.2; % assigns 11 to a.
|
| ( ) | Parentheses | a = (2+5)*3; % assigns 21 to a
b = 2+5*3; % assigns 17 to b
c = 2*(a-10); % assigns 22 to c
|
NOTE: if you are using arrays, then the / and * operators have different behavior! See the page on array arithmetic for more information.
In addition, MATLAB has many built-in functions. Type help elfun at the MATLAB command prompt for a list. Some commonly used functions are given here:
| Function | Description |
|---|---|
| cos | The cosine function |
| sin | The sine function |
| tan | The tangent function |
| sqrt | The square-root,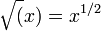 
|
| exp | The exponential function |
| log10 | The base-10 log function,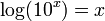 
|
| log | The natural log function,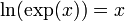 
|
| abs | The absolute value,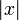 
|
M-Files
 |
|
An M-file is a series of MATLAB commands that you save in a file. Then you can re-run them easily and make changes without re-entering everything again. Anything that can be done in the command window can also be done from an m-file.
MATLAB's Path
|
|
