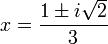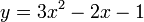Difference between revisions of "Nonlinear equations"
m (→Solution Approaches: Single Nonlinear Equation) |
|||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| + | {{Stub|section}} | ||
| Line 5: | Line 6: | ||
== Residual Form == | == Residual Form == | ||
| + | Typically when solving a nonlinear equation we solve for its ''roots'' | ||
| + | - i.e. where the equation equals zero. In some cases we want to solve | ||
| + | an equation for where <math>f(x)=\alpha</math>. In such a case, we | ||
| + | must rewrite the equation in ''residual form'': | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | |- | ||
| + | | Original Equation || Residual Form | ||
| + | | <math>f(x)=\alpha</math> || <math>r(x)=f(x)-\alpha</math> | ||
| + | |} | ||
| + | |||
| + | For example, if we wanted to solve <math>y=x^2\sin(x)</math> for the | ||
| + | value of <math>x</math> where <math>y=3</math>, we would solve for the | ||
| + | roots of the function <math>r(x)=x^2\sin(x)-3</math>. | ||
== Solving a Single Nonlinear Equation == | == Solving a Single Nonlinear Equation == | ||
| + | |||
| + | There are two general classes of techniques for solving nonlinear | ||
| + | equations: | ||
| + | |||
| + | * [[#Closed_Domain_Methods|Closed domain methods]] - These methods look for a root inside a specified interval by iteratively shrinking the interval containing the root. These methods are typically more robust than [[#Open_Domain_Methods|open domain methods]], but are somewhat slower to converge, and require that you be able to bracket the root. | ||
| + | |||
| + | * [[#Open_Domain_Methods|Open domain methods]] - These methods look for a root near a specified initial guess, but are not constrained in the region that they search for a root. These methods typically converge faster than [[#Closed_Domain_Methods|closed domain methods]], ''if'' the initial guess is "close enough" to the root. | ||
| − | === Closed Domain Methods === | + | |
| − | ==== Bisection ==== | + | === Closed Domain Methods === {{Stub|section}} ==== Bisection ==== |
==== Regula Falsi ==== | ==== Regula Falsi ==== | ||
| + | |||
| + | |||
=== Open Domain Methods === | === Open Domain Methods === | ||
| + | {{Stub|section}} | ||
==== Secant Method ==== | ==== Secant Method ==== | ||
==== Newton's Method ==== | ==== Newton's Method ==== | ||
| Line 24: | Line 48: | ||
== Solving a System of Nonlinear Equations == | == Solving a System of Nonlinear Equations == | ||
| + | {{Stub|section}} | ||
=== Newton's Method === | === Newton's Method === | ||
| + | |||
| + | |||
| Line 30: | Line 57: | ||
== Solution Approaches: Single Nonlinear Equation == | == Solution Approaches: Single Nonlinear Equation == | ||
| + | |||
=== Excel === | === Excel === | ||
| + | |||
| + | To solve a nonlinear equation in Excel, we have to options: | ||
| + | |||
| + | * [[#Goal_Seek|Goal Seek]] is a simple way to solve a single nonlinear equation. | ||
| + | |||
| + | * [[#Solver|Solver]] is a more powerful way to solve a nonlinear equation. It can also perform minimization, maximization, and can solve systems of nonlinear equations as well. | ||
| + | |||
==== Goal Seek ==== | ==== Goal Seek ==== | ||
| + | {{Stub|section}} | ||
| + | <!-- jcs need to include image of goal seek and a simple example --> | ||
| + | |||
==== Solver ==== | ==== Solver ==== | ||
| + | {{Stub|section}} | ||
| + | <!-- jcs need to include image of solver and a simple example --> | ||
| + | |||
=== Matlab === | === Matlab === | ||
| + | |||
| + | To solve a single nonlinear equation in Matlab, we use the | ||
| + | [[#FZERO|<tt>fzero</tt>]] function. If, however, we are solving for the roots | ||
| + | of a polynomial, we can use the [[#ROOTS|<tt>roots</tt>]] function. This will | ||
| + | solve for ''all'' of the polynomial roots (both real and imaginary). | ||
| + | |||
==== ROOTS ==== | ==== ROOTS ==== | ||
| + | |||
| + | The <tt>roots</tt> function can be used to obtain all of the roots | ||
| + | (both real and imaginary) of a polynomial | ||
| + | <source lang="matlab"> | ||
| + | xroots = roots( coefs ); | ||
| + | </source> | ||
| + | * <tt>coefs</tt> are the polynomial coefficients, in ''descending'' order. | ||
| + | * <tt>xroots</tt> is a vector containing all of the polynomial roots. | ||
| + | |||
| + | For example, consider the quadratic equation <math>y=3x^2-2x+1</math>. From the | ||
| + | [http://en.wikipedia.org/wiki/Quadratic_formula#Quadratic_formula quadratic formula], | ||
| + | we can identify the roots as | ||
| + | :<math> | ||
| + | x = \frac{1 \pm i\sqrt{2}}{3} | ||
| + | </math> | ||
| + | where <math>i\equiv\sqrt{-1}</math> is the imaginary number. | ||
| + | |||
| + | Using the <tt>roots</tt> function we have | ||
| + | <source lang="matlab"> | ||
| + | x = roots( [3 -2 1] ); | ||
| + | </source> | ||
| + | which gives | ||
| + | x = | ||
| + | 0.3333 + 0.4714i | ||
| + | 0.3333 - 0.4714i | ||
| + | |||
| + | This is equivalent to the answer above obtained via the quadratic formula. | ||
| + | |||
| + | |||
==== FZERO ==== | ==== FZERO ==== | ||
| + | |||
| + | In Matlab, <tt>fzero</tt> is the most flexible way to find the roots | ||
| + | of a nonlinear equation. Its syntax is slightly different depending on | ||
| + | the type of function we are using: | ||
| + | * For a function stored in an m-file named <tt>myFunction.m</tt> we use | ||
| + | :<source lang="matlab"> | ||
| + | x = fzero( 'myFunction', xguess ); | ||
| + | </source> | ||
| + | * For an [[Matlab_Functions#Anonymous_Functions|anonymous function]] named <tt>fun>/tt> | ||
| + | :<source lang="matlab"> | ||
| + | x = fzero( fun, xguess ); | ||
| + | </source> | ||
| + | * For a built in function (like <tt>sin</tt>, <tt>exp</tt>, etc.) | ||
| + | :<source lang="matlab"> | ||
| + | x = fzero( @sin, xguess ); | ||
| + | </source> | ||
| + | |||
| + | Note that <tt>fzero</tt> can only find real roots. Therefore, if we | ||
| + | tried to use it on the quadratic function <math>y=3x^2-2x+1</math>, it | ||
| + | would fail. To demonstrate its usage, let's solve for the roots of the | ||
| + | function | ||
| + | |||
| + | :<math> y=3x^2-2x-1</math> | ||
| + | |||
| + | From the quadratic formula, or by factoring this equation, we know | ||
| + | that its roots should be <math>x=-1/3</math> and <math>x=1</math>. | ||
| + | |||
| + | To use <tt>fzero</tt> to solve this, we could use an anonymous function: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | f = @(x)(3*x.^2-2*x-1); | ||
| + | x1 = fzero( f, -2 ); % start looking for the root at -2.0 | ||
| + | x2 = fzero( f, 2 ); % start looking for the root at 2.0 | ||
| + | </source> | ||
| + | |||
| + | This results in <tt>x1=-0.33333</tt> and <tt>x2=1</tt>. Note that here | ||
| + | we found the two roots by using different initial guesses. Of course | ||
| + | it helps to know where the roots are so that you can supply decent | ||
| + | initial guesses! | ||
| + | |||
| + | To solve this using a m-file, first create the function you will use: | ||
| + | {| border="1" cellpadding="5" cellspacing="0" | ||
| + | |+ style="background:lightgrey" | myQuadratic.m | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | function y = myQuadratic(x) | ||
| + | y = 3*x.^2 - 2*x -1 | ||
| + | </source> | ||
| + | |} | ||
| + | Save this in a file <tt>myQuadratic.m</tt> and then use <tt>fzero</tt>: | ||
| + | <source lang="matlab"> | ||
| + | x1 = fzero( 'myQuadratic', -2.0 ); % start looking for the root at -2.0 | ||
| + | x2 = fzero( 'myQuadratic', 2.0 ); % start looking for the root at 2.0 | ||
| + | </source> | ||
| + | |||
| + | |||
==== FMINSEARCH ==== | ==== FMINSEARCH ==== | ||
| + | |||
| + | Occasionally we want to maximize or minimize a function. Matlab | ||
| + | provides a tool called <tt>fminsearch</tt> to do this. It searches for | ||
| + | the minimum of a function near a starting guess. As with | ||
| + | [[#fzero|<tt>fzero</tt>]], you use this in different ways depending on | ||
| + | what kind of function you are minimizing: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | x = fminsearch( 'myFun', xo ); % when using a function in an m-file | ||
| + | x = fminsearch( myFun, xo ); % when using an anonymous function | ||
| + | x = fminsearch( @myFun, xo ); % when using a built-in function | ||
| + | </source> | ||
| + | |||
| + | {{Stub|section}} | ||
| + | <!-- jcs still need to provide an example and discuss maximizing functions as well. --> | ||
| + | |||
| + | |||
| + | |||
== Solution Approaches: System of Nonlinear Equations == | == Solution Approaches: System of Nonlinear Equations == | ||
| + | {{Stub|section}} | ||
| + | |||
=== Excel === | === Excel === | ||
| + | Solver... | ||
| + | |||
=== Matlab === | === Matlab === | ||
| + | <tt>fsolve</tt> | ||
Revision as of 13:20, 19 February 2009
Contents
Introduction
|
Residual Form
Typically when solving a nonlinear equation we solve for its roots
- i.e. where the equation equals zero. In some cases we want to solve
an equation for where 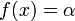 . In such a case, we
must rewrite the equation in residual form:
. In such a case, we
must rewrite the equation in residual form:
| Original Equation | Residual Form | 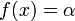 |
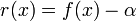
|
For example, if we wanted to solve 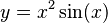 for the
value of
for the
value of 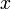 where
where 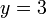 , we would solve for the
roots of the function
, we would solve for the
roots of the function 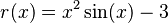 .
.
Solving a Single Nonlinear Equation
There are two general classes of techniques for solving nonlinear equations:
- Closed domain methods - These methods look for a root inside a specified interval by iteratively shrinking the interval containing the root. These methods are typically more robust than open domain methods, but are somewhat slower to converge, and require that you be able to bracket the root.
- Open domain methods - These methods look for a root near a specified initial guess, but are not constrained in the region that they search for a root. These methods typically converge faster than closed domain methods, if the initial guess is "close enough" to the root.
Closed Domain Methods
|
Regula Falsi
Open Domain Methods
|
Secant Method
Newton's Method
Solving a System of Nonlinear Equations
|
Newton's Method
Solution Approaches: Single Nonlinear Equation
Excel
To solve a nonlinear equation in Excel, we have to options:
- Goal Seek is a simple way to solve a single nonlinear equation.
- Solver is a more powerful way to solve a nonlinear equation. It can also perform minimization, maximization, and can solve systems of nonlinear equations as well.
Goal Seek
|
Solver
|
Matlab
To solve a single nonlinear equation in Matlab, we use the fzero function. If, however, we are solving for the roots of a polynomial, we can use the roots function. This will solve for all of the polynomial roots (both real and imaginary).
ROOTS
The roots function can be used to obtain all of the roots (both real and imaginary) of a polynomial
xroots = roots( coefs );
- coefs are the polynomial coefficients, in descending order.
- xroots is a vector containing all of the polynomial roots.
For example, consider the quadratic equation 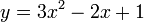 . From the
quadratic formula,
we can identify the roots as
. From the
quadratic formula,
we can identify the roots as
where 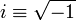 is the imaginary number.
is the imaginary number.
Using the roots function we have
x = roots( [3 -2 1] );
which gives
x = 0.3333 + 0.4714i 0.3333 - 0.4714i
This is equivalent to the answer above obtained via the quadratic formula.
FZERO
In Matlab, fzero is the most flexible way to find the roots of a nonlinear equation. Its syntax is slightly different depending on the type of function we are using:
- For a function stored in an m-file named myFunction.m we use
x = fzero( 'myFunction', xguess );
- For an anonymous function named fun>/tt>
x = fzero( fun, xguess );
- For a built in function (like <tt>sin, exp, etc.)
x = fzero( @sin, xguess );
Note that fzero can only find real roots. Therefore, if we
tried to use it on the quadratic function 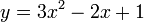 , it
would fail. To demonstrate its usage, let's solve for the roots of the
function
, it
would fail. To demonstrate its usage, let's solve for the roots of the
function
From the quadratic formula, or by factoring this equation, we know
that its roots should be 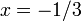 and
and 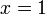 .
.
To use fzero to solve this, we could use an anonymous function:
f = @(x)(3*x.^2-2*x-1);
x1 = fzero( f, -2 ); % start looking for the root at -2.0
x2 = fzero( f, 2 ); % start looking for the root at 2.0
This results in x1=-0.33333 and x2=1. Note that here we found the two roots by using different initial guesses. Of course it helps to know where the roots are so that you can supply decent initial guesses!
To solve this using a m-file, first create the function you will use:
function y = myQuadratic(x)
y = 3*x.^2 - 2*x -1
|
Save this in a file myQuadratic.m and then use fzero:
x1 = fzero( 'myQuadratic', -2.0 ); % start looking for the root at -2.0
x2 = fzero( 'myQuadratic', 2.0 ); % start looking for the root at 2.0
FMINSEARCH
Occasionally we want to maximize or minimize a function. Matlab provides a tool called fminsearch to do this. It searches for the minimum of a function near a starting guess. As with fzero, you use this in different ways depending on what kind of function you are minimizing:
x = fminsearch( 'myFun', xo ); % when using a function in an m-file
x = fminsearch( myFun, xo ); % when using an anonymous function
x = fminsearch( @myFun, xo ); % when using a built-in function
|
Solution Approaches: System of Nonlinear Equations
|
Excel
Solver...
Matlab
fsolve