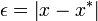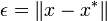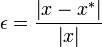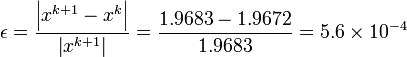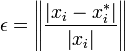Difference between revisions of "Iteration and Convergence"

From Sutherland_wiki
Jump to: navigation, search
(first pass at tolerances and norms. Needs more work!)
 
(No difference)

Latest revision as of 13:55, 29 August 2009

Iterative Techniques

Iterative techniques are based on a refinement of a guessed quantity until it is "sufficiently accurate." The question becomes: how do we measure error to determine when our iterative solution is "close enough?"

There are two categories of error metrics:

  • Absolute error
  • Relative error

These will be discussed below.


Vector Norms

Vector norms are measures of the "size" of a vector. There are several commonly used vector norms, summarized in the following table:

Definition of common error norms
Norm Definition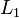
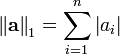
L_1 \left\Vert \mathbf{a} \right\Vert_{1} = \sum_{i=1}^{n} \left| a_i \right|
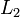
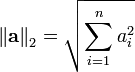
L_2 \left\Vert \mathbf{a} \right\Vert_{2} = \sqrt{ \sum_{i=1}^{n} a_i^2 }
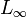
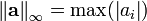
L_\infty \left\Vert \mathbf{a} \right\Vert_\infty = \max (\left|a_{i}\right|)

Note that the 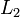L_2 norm is the length of a vector.


Absolute Error

An absolute error is a measure of the absolute difference between two quantities. For example,

\epsilon = \left| x - x^\ast \right|

is an absolute error or difference between 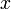x and x^\ast

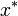
For vectors, we simply use a vector norm,

\epsilon = \left\Vert x - x^\ast \right\Vert

In both cases, \epsilon is a scalar quantity.


Relative Error

Relative error takes a normalized difference between two quantities:

\epsilon = \frac{\left|x - x^\ast\right|}{\left|x\right|}

Of course, we need to be careful that 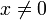x\ne 0 in the equation above. The nice thing about relative error is that it can be used to determine how many digits of accuracy there is in an answer without regard for the magnitude of the values themselves.

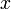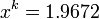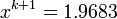For example, if we have two successive iterations in a solution for x: x^{k}=1.9672 and x^{k+1}=1.9683 then we could determine how many digits are not changing by

\epsilon = \frac{\left|x^{k+1}-x^k\right|}{\left|x^{k+1}\right|} = \frac{ 1.9683 - 1.9672}{1.9683} = 5.6\times 10^{-4}

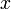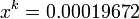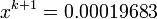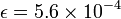
The nice thing is that if we had much smaller values of x, x^{k}=0.00019672 and x^{k+1}=0.00019683 we obtain the same error estimate: \epsilon = 5.6\times 10^{-4}

Vectors

For two vectors, we can determine a relative error tolerance by

\epsilon = \left\Vert \frac{\left|x_i - x_i^\ast\right|}{\left|x_i\right|} \right\Vert

A matlab code to do this for two vectors x and xold would look like 

 err = norm( abs(x - xold)./abs(x), 2 );

This calculates the 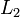L_2 norm. See "help norm" in matlab for more information on calculating other norms.


Convergence

Warn.jpg
This section is a stub and needs to be expanded.
If you can provide information or finish this section you're welcome to do so and then remove this message afterwards.
Retrieved from "https://sutherland.che.utah.edu/wiki/index.php?title=Iteration_and_Convergence&oldid=428"