Difference between revisions of "Matlab Arrays"
(→Array Basics) |
|||
| Line 3: | Line 3: | ||
== Array Basics == | == Array Basics == | ||
An array is an ''n''-dimensional collection of numbers. [[LinearAlgebra#Basics: Matrices & Vectors|Matrices]] are 2-dimensional arrays, and [[LinearAlgebra#Basics: Matrices & Vectors|vectors]] are 1-dimensional arrays. | An array is an ''n''-dimensional collection of numbers. [[LinearAlgebra#Basics: Matrices & Vectors|Matrices]] are 2-dimensional arrays, and [[LinearAlgebra#Basics: Matrices & Vectors|vectors]] are 1-dimensional arrays. | ||
| + | |||
| + | Vectors can be either a row or column vector: | ||
| + | <center> | ||
| + | <math> | ||
| + | \quad | ||
| + | a=\left[ \begin{array}{c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array} \right] | ||
| + | \quad | ||
| + | b = \left[ \begin{array}{cccc} b_1 & b_2 & \cdots & b_n \end{array} \right] | ||
| + | \quad | ||
| + | c = \left[ \begin{array}{c} 1 \\ 4 \\ 3.2 \\ \pi \end{array} \right] | ||
| + | </math> | ||
| + | </center> | ||
| + | We refer to the elements of an array by their position in the array. For example, the third element in <math>c</math> is 3.2, and the second element in <math>a</math> is <math>a_2</math>. | ||
| + | |||
| + | Matrices are two-dimensional arrays, whose elements are referred to by the ''row'' and ''column'' that they belong to. For example, | ||
| + | <center> | ||
| + | <math> | ||
| + | \quad | ||
| + | A = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right] | ||
| + | </math> | ||
| + | </center> | ||
| + | is a matrix with three rows and two columns. We refer to this as a <math>\\scriptstyls 3 \times 2</math> matrix. The first index is the row and the second index is the column. | ||
| + | |||
| + | === Transposing Arrays === | ||
| + | Occasionally we want to ''transpose'' an array. This is done by exchanging rows and columns. For example, | ||
| + | <center> | ||
| + | <math> | ||
| + | A = \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{array} \right] | ||
| + | \quad \Rightarrow \quad | ||
| + | A^\mathsf{T} = \left[ \begin{array}{ccc} 2 & 6 & 10 \\ 4 & 8 & 12 \end{array} \right] | ||
| + | </math> | ||
| + | </center> | ||
| + | Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | ||
== Creating Vectors == | == Creating Vectors == | ||
Revision as of 07:25, 29 July 2008
Array Basics
An array is an n-dimensional collection of numbers. Matrices are 2-dimensional arrays, and vectors are 1-dimensional arrays.
Vectors can be either a row or column vector:
![\quad
a=\left[ \begin{array}{c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array} \right]
\quad
b = \left[ \begin{array}{cccc} b_1 & b_2 & \cdots & b_n \end{array} \right]
\quad
c = \left[ \begin{array}{c} 1 \\ 4 \\ 3.2 \\ \pi \end{array} \right]](/wiki/images/math/e/4/3/e43e1854d9671047aacec1ea8597f8d6.png)
We refer to the elements of an array by their position in the array. For example, the third element in 
is 3.2, and the second element in 
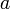is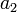 
.
Matrices are two-dimensional arrays, whose elements are referred to by the row and column that they belong to. For example,
![\quad
A = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right]](/wiki/images/math/d/d/6/dd6c2781d1295794d3e3283ec200032b.png)
is a matrix with three rows and two columns. We refer to this as a Failed to parse (syntax error): \\scriptstyls 3 \times 2 matrix. The first index is the row and the second index is the column.
Transposing Arrays
Occasionally we want to transpose an array. This is done by exchanging rows and columns. For example,
![A = \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{array} \right]
\quad \Rightarrow \quad
A^\mathsf{T} = \left[ \begin{array}{ccc} 2 & 6 & 10 \\ 4 & 8 & 12 \end{array} \right]](/wiki/images/math/0/e/b/0eb7535c826df9c92c3cf1d2939d48c7.png)
Here the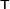 
superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, 
.
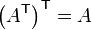