Difference between revisions of "Matlab Arrays"
m (→Array Basics) |
(→Creating Vectors) |
||
| Line 37: | Line 37: | ||
Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | ||
| − | == Creating Vectors == | + | == Creating Vectors in Matlab == |
| + | |||
=== Manually Creating Vectors === | === Manually Creating Vectors === | ||
| + | Often we need to create small vectors with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. For example, to create the vector | ||
| + | <math> | ||
| + | a = \left[ \begin{array}{cc} 2 \\ 4 \\ 6 \\ 8 \end{array} \right] | ||
| + | </math> | ||
| + | we could use any of the following Matlab commands: | ||
| + | a = [ 2; 4; 6; 8; ]; % create a column vector | ||
| + | a = [ 2 4 6 8 ]'; % create a row vector and then | ||
| + | % transpose it to produce a column vector. | ||
| + | a = [ 2 | ||
| + | 4 | ||
| + | 6 | ||
| + | 8 ]; % creates a column vector. | ||
| + | Similarly, a row vector such as b = [1 3 5 7 ] may be created as | ||
| + | b = [ 1 3 5 7 ]; | ||
| + | b = [ 1, 3, 5, 7 ]; | ||
| + | b = [ 1; 3; 5; 7 ]'; % transpose a column vector. | ||
| + | |||
| + | Note that the semicolon (;) instructs Matlab that we have the end of a row in the matrix. Commas may be used to separate columns in the matrix, but they are not necessary. | ||
| + | |||
| + | |||
=== Using the ":" operator to create arrays === | === Using the ":" operator to create arrays === | ||
| + | Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The ''':''' operator can help us create such arrays: | ||
| + | |||
| + | array = lower : increment : upper; | ||
| + | This creates an array starting at ''lower'' and ending at ''upper'' with spacing of ''increment''. You may eliminate the ''increment'' argument, in which case it defaults to 1. | ||
| + | |||
| + | Examples: | ||
| + | a = 1:5; % creates a=[ 1 2 3 4 5 ] | ||
| + | b = 1:1:5; % creates b=[ 1 2 3 4 5 ] | ||
| + | c = 1:2:7; % creates c=[ 1 3 5 7 ] | ||
| + | d = 1:2:8; % creates d=[ 1 3 5 7 ] | ||
| + | e = 1.1:5 % creates e=[ 1.1 2.3 3.1 4.1 ] | ||
| + | f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ] | ||
| + | g = 5:-1:1; % creates g=[ 5 4 3 2 1 ]; | ||
| + | h = (1:3)'; % creates a column vector with elements 1, 2, 3. | ||
| + | |||
| + | |||
=== Linspace and Logspace === | === Linspace and Logspace === | ||
| + | Occasionally we want to create numbers that are equally spaced between two limits. We can use the ''linspace'' command to do this. | ||
| + | |||
| + | linspace( lo, hi, n ); | ||
| + | Creates a row vector with ''n'' points equally spaced between ''lo'' and ''hi''. | ||
| + | |||
| + | Examples: | ||
| + | a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ] | ||
| + | b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ] | ||
| + | c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ] | ||
| + | d = linspace(1,5,5)'; % creates a column vector | ||
| + | |||
| + | Sometimes we want points logarithmically spaced. For example, we may want to create a vector a=[ 0.1 1 10 100]. This can be accomplished using the ''logspace'' command: | ||
| + | logspace( lo, hi, n ); | ||
| + | Creates a vector with ''n'' points spaced logarithmically between <math>10^\mathrm{lo}</math> and <math>10^\mathrm{hi}</math> | ||
| + | Examples: | ||
| + | a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ] | ||
| + | b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ] | ||
| + | c = logspace(-1,3,5)'; % creates a column vector | ||
== Creating Matrices == | == Creating Matrices == | ||
Revision as of 07:14, 29 July 2008
Array Basics
An array is an n-dimensional collection of numbers. Matrices are 2-dimensional arrays, and vectors are 1-dimensional arrays.
Vectors can be either a row or column vector:
![\quad
a=\left[ \begin{array}{c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array} \right]
\quad
b = \left[ \begin{array}{cccc} b_1 & b_2 & \cdots & b_n \end{array} \right]
\quad
c = \left[ \begin{array}{c} 1 \\ 4 \\ 3.2 \\ \pi \end{array} \right]](/wiki/images/math/e/4/3/e43e1854d9671047aacec1ea8597f8d6.png)
We refer to the elements of an array by their position in the array. For example, the third element in  is 3.2, and the second element in
is 3.2, and the second element in 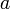 is
is 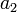 .
.
Matrices are two-dimensional arrays, whose elements are referred to by the row and column that they belong to. For example,
![\quad
A = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right]](/wiki/images/math/d/d/6/dd6c2781d1295794d3e3283ec200032b.png)
is a matrix with three rows and two columns. We refer to this as a 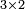 matrix. The first index is the row and the second index is the column.
matrix. The first index is the row and the second index is the column.
Transposing Arrays
Occasionally we want to transpose an array. This is done by exchanging rows and columns. For example,
![A = \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{array} \right]
\quad \Rightarrow \quad
A^\mathsf{T} = \left[ \begin{array}{ccc} 2 & 6 & 10 \\ 4 & 8 & 12 \end{array} \right]](/wiki/images/math/0/e/b/0eb7535c826df9c92c3cf1d2939d48c7.png)
Here the 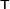 superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words,
superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, 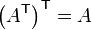 .
.
Creating Vectors in Matlab
Manually Creating Vectors
Often we need to create small vectors with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. For example, to create the vector
![a = \left[ \begin{array}{cc} 2 \\ 4 \\ 6 \\ 8 \end{array} \right]](/wiki/images/math/e/f/d/efd67bf3a30e385857ea9949bbd21c84.png) we could use any of the following Matlab commands:
we could use any of the following Matlab commands:
a = [ 2; 4; 6; 8; ]; % create a column vector
a = [ 2 4 6 8 ]'; % create a row vector and then
% transpose it to produce a column vector.
a = [ 2
4
6
8 ]; % creates a column vector.
Similarly, a row vector such as b = [1 3 5 7 ] may be created as
b = [ 1 3 5 7 ]; b = [ 1, 3, 5, 7 ]; b = [ 1; 3; 5; 7 ]'; % transpose a column vector.
Note that the semicolon (;) instructs Matlab that we have the end of a row in the matrix. Commas may be used to separate columns in the matrix, but they are not necessary.
Using the ":" operator to create arrays
Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The : operator can help us create such arrays:
array = lower : increment : upper;
This creates an array starting at lower and ending at upper with spacing of increment. You may eliminate the increment argument, in which case it defaults to 1.
Examples:
a = 1:5; % creates a=[ 1 2 3 4 5 ] b = 1:1:5; % creates b=[ 1 2 3 4 5 ] c = 1:2:7; % creates c=[ 1 3 5 7 ] d = 1:2:8; % creates d=[ 1 3 5 7 ] e = 1.1:5 % creates e=[ 1.1 2.3 3.1 4.1 ] f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ] g = 5:-1:1; % creates g=[ 5 4 3 2 1 ]; h = (1:3)'; % creates a column vector with elements 1, 2, 3.
Linspace and Logspace
Occasionally we want to create numbers that are equally spaced between two limits. We can use the linspace command to do this.
linspace( lo, hi, n ); Creates a row vector with n points equally spaced between lo and hi.
Examples:
a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ] b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ] c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ] d = linspace(1,5,5)'; % creates a column vector
Sometimes we want points logarithmically spaced. For example, we may want to create a vector a=[ 0.1 1 10 100]. This can be accomplished using the logspace command:
logspace( lo, hi, n ); Creates a vector with n points spaced logarithmically betweenand
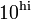
Examples:
a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ] b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ] c = logspace(-1,3,5)'; % creates a column vector