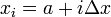Numerical Integration
From Sutherland_wiki
|
Contents
Introduction
Midpoint Rule
Example
Trapezoid Rule
Example
Simpson's 1/3 Rule
Example
Summary of Common Quadrature Formulas
| Name | Formula | Comments |
|---|---|---|
| Midpoint Rule | 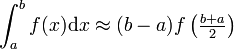
|
|
| Trapezoid Rule | ![\int_{a}^{b} f(x) \mathrm{d} x \approx \tfrac{b-a}{2} \left[ f(b)+f(a) \right]](/wiki/images/math/0/f/c/0fc354ac2c1823ba9b99dfa737d052d1.png)
|
|
| Simpson's 1/3 Rule | ![\int_a^b f(x) \mathrm d x \approx \tfrac{\Delta x}{3} \left[ f(a) +4f\left(\tfrac{a+b}{2}\right) + f(b) \right]](/wiki/images/math/e/c/7/ec7275740d9502d428f396e4483e9a06.png)
|
|
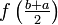
![[a,b]](/wiki/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png)
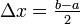 and
and