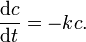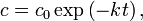ODEs

Solving ODEs in Matlab

To solve an ODE (or a system of ODEs) in Matlab, you need to build a function that evaluates the right-hand-side of the ODEs. For example, let's consider a simple ODE that describes first-order decay

$\frac{\mathrm{d}c}{\mathrm{d}t} = -kc.$

This can easily be separated and solved analytically to find

$c = c_0 \exp\left(-kt\right),$

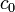where $c_0$ is the concentration at $t=0$.

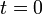To solve this in Matlab, we create a function like the following:

decay.m

function rhs = decay( k, c ) % calculates the rate of decay given the % rate constant (k) and concentration (c) rhs = -k*t;

The ODE solvers in Matlab have the following requirements:

• Provide a function that calculates the RHS of the ODE. This function must take two arguments: the independent variable (e.g. time), and the dependent variable(s).
• Provide the time interval over which you desire the solution.
• Provide the value of the dependent variables at the beginning of the time interval (the initial condition).

We can now solve our problem above using the function contained in decay.m to integrate this ODE. The Matlab code to do this is outlined below.

c0 = 10; k = 0.1; Define the initial concentration and rate constant. rhsfun = @(t,c)( decay(k,c) ); Define a dummy anonymous function that can be used with Matlab's time integrator. This function simply calls through to the decay function defined above, supplying the appropriate arguments. The arguments of rhsfun are mandated by Matlab's ODE solver. [t,c] = ode45( rhsfun, [0,50], c0 ); Solve the ODE on the interval [0,50]. The solution is stored in the vectors t and c. plot(t,c); xlabel('t'); ylabel('c'); Plot the concentration as a function of time.

Of course, for this ODE we could solve this without a separate function for the RHS as follows:

c0 = 10; k = 0.1; rhs = @(t,c)( -k*c ); [time,conc] = ode45( rhs, [0,50], c0 ); plot(time,conc); xlabel('t'); ylabel('c');

Systems of ODEs in Matlab

This section is a stub and needs to be expanded. If you can provide information or finish this section you're welcome to do so and then remove this message afterwards.