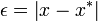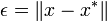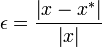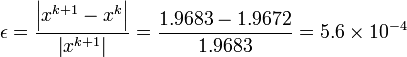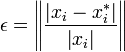Iteration and Convergence
Contents
Iterative Techniques
Iterative techniques are based on a refinement of a guessed quantity until it is "sufficiently accurate." The question becomes: how do we measure error to determine when our iterative solution is "close enough?"
There are two categories of error metrics:
- Absolute error
- Relative error
These will be discussed below.
Vector Norms
Vector norms are measures of the "size" of a vector. There are several commonly used vector norms, summarized in the following table:
Definition of common error norms Norm Definition 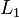
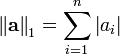
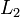
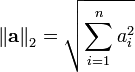
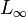
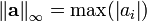
Note that the 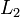 norm is the length of a vector.
norm is the length of a vector.
Absolute Error
An absolute error is a measure of the absolute difference between two quantities. For example,
is an absolute error or difference between 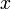 and
and 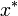
For vectors, we simply use a vector norm,
In both cases,  is a scalar quantity.
is a scalar quantity.
Relative Error
Relative error takes a normalized difference between two quantities:
Of course, we need to be careful that 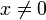 in the
equation above. The nice thing about relative error is that it can be
used to determine how many digits of accuracy there is in an answer
without regard for the magnitude of the values themselves.
in the
equation above. The nice thing about relative error is that it can be
used to determine how many digits of accuracy there is in an answer
without regard for the magnitude of the values themselves.
For example, if we have two successive iterations in a solution for
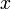 :
: 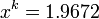 and
and
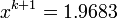 then we could determine how many digits
are not changing by
then we could determine how many digits
are not changing by
The nice thing is that if we had much smaller values of
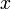 ,
, 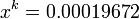 and
and
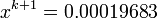 we obtain the same error estimate:
we obtain the same error estimate:
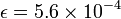
Vectors
For two vectors, we can determine a relative error tolerance by
A matlab code to do this for two vectors x and xold would look like
err = norm( abs(x - xold)./abs(x), 2 );
This calculates the 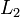 norm. See "help norm" in matlab
for more information on calculating other norms.
norm. See "help norm" in matlab
for more information on calculating other norms.
Convergence
|