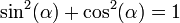Matlab Arrays
Array Basics
An array is an n-dimensional collection of numbers. Matrices are 2-dimensional arrays, and vectors are 1-dimensional arrays.
Vectors can be either a row or column vector:
![\quad
a=\left[ \begin{array}{c} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{array} \right]
\quad
b = \left[ \begin{array}{cccc} b_1 & b_2 & \cdots & b_n \end{array} \right]
\quad
c = \left[ \begin{array}{c} 1 \\ 4 \\ 3.2 \\ \pi \end{array} \right]](/wiki/images/math/e/4/3/e43e1854d9671047aacec1ea8597f8d6.png)
We refer to the elements of an array by their position in the array. For example, the third element in  is 3.2, and the second element in
is 3.2, and the second element in 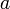 is
is 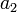 .
.
Matrices are two-dimensional arrays, whose elements are referred to by the row and column that they belong to. For example,
![\quad
A = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right]](/wiki/images/math/d/d/6/dd6c2781d1295794d3e3283ec200032b.png)
is a matrix with three rows and two columns. We refer to this as a 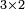 matrix. The first index is the row and the second index is the column.
matrix. The first index is the row and the second index is the column.
Transposing Arrays
Occasionally we want to transpose an array. This is done by exchanging rows and columns. For example,
![A = \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{array} \right]
\quad \Rightarrow \quad
A^\mathsf{T} = \left[ \begin{array}{ccc} 2 & 6 & 10 \\ 4 & 8 & 12 \end{array} \right]](/wiki/images/math/0/e/b/0eb7535c826df9c92c3cf1d2939d48c7.png)
Here the 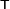 superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words,
superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, 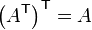 .
.
Creating Arrays in Matlab
Manual Creation
Often we need to create small arrays with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. For example, to create the vector
![a = \left[ \begin{array}{cc} 2 \\ 4 \\ 6 \\ 8 \end{array} \right]](/wiki/images/math/e/f/d/efd67bf3a30e385857ea9949bbd21c84.png) we could use any of the following Matlab commands:
we could use any of the following Matlab commands:
a = [ 2; 4; 6; 8; ]; % create a column vector
a = [ 2 4 6 8 ]'; % create a row vector and then
% transpose it to produce a column vector.
a = [ 2
4
6
8 ]; % creates a column vector.
Similarly, a row vector such as b = [1 3 5 7 ] may be created as
b = [ 1 3 5 7 ]; b = [ 1, 3, 5, 7 ]; b = [ 1; 3; 5; 7 ]'; % transpose a column vector.
Note that the semicolon (;) identifies the end of a row in the matrix. Commas may be used to separate columns in the matrix, but they are not necessary.
Matrices may be created directly in much the same way as vectors are. As an example, let's build the matrix ![A = \left[ \begin{array}{cc} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{array} \right]](/wiki/images/math/b/5/d/b5deec6c820cdd2759fdadfbdcbf8cb2.png) . This may be done in several ways.
. This may be done in several ways.
A = [ 2 4; 6 8; 10 12 ];
A = [ 2 4
6 8
10 12 ];
Note that a semicolon (;) separates each row of the matrix while spaces separate each column.
We may also create a matrix from vectors. For example, we may construct A from its rows as follows:
arow1 = [ 2 4 ]; arow2 = [ 6 8 ]; arow3 = [ 10 12 ]; A = [ arow1; arow2; arow3 ];
Similarly, we can build a matrix from its columns:
acol1 = [2 6 10]'; acol2 = [4; 8; 12]; A = [ acol1 acol2 ];
Using the ":" operator to create arrays
Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The : operator can help us create such arrays:
array = lower : increment : upper;
This creates an array starting at lower and ending at upper with spacing of increment. You may eliminate the increment argument, in which case it defaults to 1.
Examples:
a = 1:5; % creates a=[ 1 2 3 4 5 ] b = 1:1:5; % creates b=[ 1 2 3 4 5 ] c = 1:2:7; % creates c=[ 1 3 5 7 ] d = 1:2:8; % creates d=[ 1 3 5 7 ] e = 1.1:5 % creates e=[ 1.1 2.3 3.1 4.1 ] f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ] g = 5:-1:1; % creates g=[ 5 4 3 2 1 ]; h = (1:3)'; % creates a column vector with elements 1, 2, 3.
Linspace and Logspace
Occasionally we want to create numbers that are equally spaced between two limits. We can use the linspace command to do this.
linspace( lo, hi, n ); Creates a row vector with n points equally spaced between lo and hi.
Examples:
a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ] b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ] c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ] d = linspace(1,5,5)'; % creates a column vector
Sometimes we want points logarithmically spaced. For example, we may want to create a vector a=[ 0.1 1 10 100]. This can be accomplished using the logspace command:
logspace( lo, hi, n ); Creates a vector with n points spaced logarithmically betweenand
Examples:
a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ] b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ] c = logspace(-1,3,5)'; % creates a column vector
Shortcuts for Special Matrices
- ones(nrow,ncol) - creates an array of all ones with nrow rows and ncol columns.
- zeros(nrow,ncol) - creates an array of all zeros with nrow rows and ncol columns.
- eye(nrow,ncol) - creates an array with ones on its diagonal and zeros elsewhere. Example: eye(3,2) produces
![\left[ \begin{array}{cc}
1 & 0 \\
0 & 1 \\
0 & 0
\end{array} \right]](/wiki/images/math/1/5/f/15fb8ab96aeb7c71d1307fb88e4a99c2.png) while eye(3,3) gives
while eye(3,3) gives ![\left[ \begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0\\
0 & 0 & 1
\end{array} \right]](/wiki/images/math/5/8/4/584b7f33e98b96f8794e6b9f5d233913.png)
- rand(nrow,ncol) - creates an array with nrow rows and ncol columns full of random numbers.
Sparse Matrices
Accessing Arrays
Indexing arrays
Slicing arrays using the ":" operator
Information about Arrays
- size - returns the number of rows and columns in an array. Example:
A = [1 2 3; 4 5 6]; [nrow,ncol] = size(A); The result of this is that nrow=2 and ncol=3.
- length - returns the number of elements in a vector. Example:
a = [1 2 3 4 3 2 1]; na = length(a); Results in na=7.
- max For a vector, max(v) returns the largest element in v. For matrices, max(V) returns a row vector whose elements contain the maximum value in each column of V.
- min Analogous to max.
Other Useful Tools
Use MATLAB's help command to learn more about how to use these commands.
| Matlab command | Summary | Example(s) |
|---|---|---|
| sum |
|
a=sum([1 2 3]); % a=6 b=sum([1 2; 3 4]); % b = [4 6] |
| sort | Sort an array in ascending or descending order. | sort([2 5 1]) gives 1 2 5 |
| any | any(A) Evaluates to "true" if any of the elements in the array are true (nonzero). |
a=[1 2 3]; b=[1 3 4]; r1 = any(a>b); % r1 is FALSE (equal to 0) r2 = any(a==b); % r2 is TRUE (equal to 1) since a(1) is equal to b(1). |
| all | Evaluates to "true" if all of the elements in the array are true (nonzero). |
A = [1 2; 3 4];
B = [-1 1; 2 3];
r1 = all(A>B); % r1 is TRUE (equal to 1) since the elements in A are
% all greater than their corresponding elements in B.
r2 = all(2*B>A); % r2 is FALSE
|
| find | find(A) returns the indices where A is nonzero. |
A = [1 5 0; 0 2 0]; i = find(A(:,1)); % i=1 i = find(A(:,2)); % i=[1 2]' i = find(A); % i=[1 3 4]' [i,j] = find(A); % i=[ 1 1 2 ]' j=[ 1 2 2 ]' i = find(A>4); % i=3 [i,j] = find(A<2); % i=[1 2 1 2]' j=[1 1 3 3]' |
| isequal | isequal(A,B) returns true if all elements of A and B are equal, false otherwise. |
A = [1 2; 3 4]; B = [2 4; 6 8]; c = isequal(A,B); % c is FALSE d = isequal(2*A,B); % d is TRUE Here is something a bit more complex, using the fact that x = rand(5); y1 = sin(x).*sin(x); z1 = cos(x).*cos(x); q = ones(5); c = isequal(q,y1+z1); % c is TRUE |