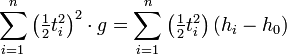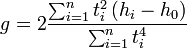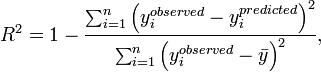Difference between revisions of "Regression"
m |
m |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | {{ | + | == Introduction == |
| + | |||
| + | Often time we measure some observable <math>\phi</math> as a function | ||
| + | of some independent variable, <math>x</math>, and we have some | ||
| + | theoretical function that we expect the observations to obey. The | ||
| + | function may have parameters in it that we need to determine. The | ||
| + | process of determining the best values of the parameters that fit the | ||
| + | function to the given data is known as ''regression''. | ||
| + | |||
| + | |||
| + | === Example === | ||
| + | |||
| + | Consider the | ||
| + | [http://en.wikipedia.org/wiki/Arrhenius_equation Arrhenius equation] | ||
| + | commonly used to describe the rate constant in chemistry, | ||
| + | |||
| + | :<math>k = A \exp \left(-\frac{E_a}{RT} \right)</math> | ||
| + | |||
| + | where | ||
| + | * <math>k</math> is the [http://en.wikipedia.org/wiki/Rate_constant rate constant] of the chemical reaction, | ||
| + | * <math>A</math> is the [http://en.wikipedia.org/wiki/Pre-exponential_factor pre-exponential factor] | ||
| + | * <math>E_a</math> is the [http://en.wikipedia.org/wiki/Activation_energy activation energy], | ||
| + | * <math>R</math> is the [http://en.wikipedia.org/wiki/Gas_constant gas constant] | ||
| + | * <math>T</math> is the temperature. | ||
| + | |||
| + | If we measured <math>k</math> as a function of <math>T</math> we could | ||
| + | determine <math>A</math> and <math>E_a</math> using regression. | ||
| − | |||
== Linear Least Squares Regression == | == Linear Least Squares Regression == | ||
| − | === The | + | Linear Least Squares Regression can be applied if we can write our |
| − | ==== | + | function in polynomial form, <math>y(x)= a_0 + a_1 x + a_2 x^2 + |
| + | \cdots + a_n x^m</math>. If we can do this, then we are looking for | ||
| + | the coefficients of the polynomial, <math>a_j</math> given | ||
| + | <math>n</math> observations <math>(x_i,y_i)</math>. We can write | ||
| + | this as | ||
| + | :<math> | ||
| + | \begin{align} | ||
| + | y_1 &= a_0 + a_1 x_1 + a_2 x_1^2 + \cdots + a_m x_1^m \\ | ||
| + | y_2 &= a_0 + a_1 x_2 + a_2 x_2^2 + \cdots + a_m x_2^m \\ | ||
| + | \vdots &= \vdots \\ | ||
| + | y_n &= a_0 + a_1 x_n + a_2 x_n^2 + \cdots + a_m x_n^m \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | or, in [[Linear_Algebra#Linear_Systems_of_Equations|matrix form]], | ||
| + | :<math> | ||
| + | \underbrace{ \left[ \begin{array}{ccccc} | ||
| + | 1 & x_1 & x_1^2 & \cdots & x_1^m \\ | ||
| + | 1 & x_2 & x_2^2 & \cdots & x_2^m \\ | ||
| + | \vdots & \vdots & \cdots & \vdots \\ | ||
| + | 1 & x_n & x_n^2 & \cdots & x_n^m | ||
| + | \end{array} \right] }_{A} | ||
| + | \underbrace{ \left( \begin{array}{c} | ||
| + | a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_m | ||
| + | \end{array}\right) }_{\phi} | ||
| + | = | ||
| + | \underbrace{ \left( \begin{array}{c} | ||
| + | y_1 \\ y_2 \\ \vdots \\ y_n | ||
| + | \end{array}\right) }_{b} | ||
| + | </math> | ||
| + | |||
| + | Regression applies when <math>n>m</math>. In other words, when we have | ||
| + | many more equations than we have unknowns. In this case, the | ||
| + | ''least-squares solution'' is written as | ||
| + | |||
| + | :<math>A^\mathsf{T}A \phi = A^\mathsf{T} b</math> | ||
| + | |||
| + | |||
| + | |||
| + | === Example === | ||
| + | |||
| + | Let's illustrate linear least squares regression with our | ||
| + | [[#Example | example above]]. First, we must rewrite the problem: | ||
| + | :<math>\begin{align} | ||
| + | k &= A \exp \left(-\frac{E_a}{RT} \right) \\ | ||
| + | \ln k &= \ln A - \frac{E_a}{RT} | ||
| + | \end{align}</math> | ||
| + | |||
| + | Note that this now looks like a polynomial, <math>y=a_0+a_1 x</math>, | ||
| + | where <math>y \equiv \ln k</math>, <math>a_0 \equiv \ln A </math>, | ||
| + | <math>a_1 \equiv E_a</math>, and <math>x \equiv -1/(RT)</math>. | ||
| + | |||
| + | If we write these equations for each of our <math>n</math> data points | ||
| + | in matrix form we obtain | ||
| + | :<math> | ||
| + | \underbrace{ \left[ \begin{array}{cc} | ||
| + | 1 & \frac{-1}{RT_1} \\ 1 & \frac{-1}{RT_2} \\ 1 & \frac{-1}{RT_3} \\ \vdots & \vdots \\ 1 & \frac{-1}{RT_n} | ||
| + | \end{array} \right] }_{A} | ||
| + | \underbrace{ \left(\begin{array}{c} | ||
| + | a_0 \\ a_1 | ||
| + | \end{array}\right) }_{\phi} | ||
| + | \underbrace{ \left(\begin{array}{c} | ||
| + | \ln k_1 \\ \ln k_2 \\ \ln k_3 \\ \vdots \\ \ln k_n | ||
| + | \end{array}\right) }_{b} | ||
| + | </math> | ||
| + | and the equations to be solved are | ||
| + | :<math>A^\mathsf{T}A\phi=A^\mathsf{T}b</math> | ||
| + | |||
| + | Note that since <math>A</math> is a 2x<math>n</math> matrix and | ||
| + | <math>b</math> is a <math>n</math>x1 vector, we have a 2x2 system of | ||
| + | equations to solve (see notes on | ||
| + | [[Linear_Algebra#Matrix-Matrix_Product|matrix multiplication]]). | ||
| + | |||
| + | |||
| + | |||
| + | === Example 2 === | ||
| + | |||
| + | Let's consider another example, where we want to determine the value | ||
| + | of the gravitational constant, <math>g</math>, via regression. To do | ||
| + | this, we could drop an object from a set height, <math>h_0</math> at | ||
| + | time <math>t=0</math> and measure its height as a function of time. | ||
| + | Neglecting air resistance, we have | ||
| + | |||
| + | :<math>h=h_0 + v_0 t + \tfrac{1}{2}gt^2</math> | ||
| + | |||
| + | where <math>g=-9.8</math> m/s<sup>2</sup> is the gravitational | ||
| + | constant. Assume that <math>h_0=10</math> meters is known precisely, | ||
| + | and that since we drop the ball from rest, <math>v_0=0</math> m/s. The | ||
| + | data we collect is given in the table below: | ||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
| + | |+ '''Height as a function of time''' | ||
| + | |- | ||
| + | | '''time (s)''' || 0.08 || 0.28 || 0.48 || 0.53 || 0.70 || 1.05 || 1.31 || 1.36 | ||
| + | |- | ||
| + | | '''h(m)''' || 9.90 || 9.58 || 8.86 || 8.76 || 7.58 || 4.71 || 1.47 || 1.01 | ||
| + | |} | ||
| + | |||
| + | Let's go through this problem by hand: | ||
| + | <ol> | ||
| + | |||
| + | <li> First, we rearrange our equation as follows: | ||
| + | :<math> h-h_0 = \tfrac{1}{2}gt^2</math> | ||
| + | now we are left with an equation of the form <math>y=ax</math>. | ||
| + | </li> | ||
| + | |||
| + | <li> Write down the equations in matrix form, one equation for each of | ||
| + | the <math>n</math> data points. | ||
| + | :<math> | ||
| + | \underbrace{ | ||
| + | \left[\begin{array}{c} | ||
| + | \tfrac{1}{2}t_1^2 \\ \tfrac{1}{2}t_2^2 \\ \vdots \\ \tfrac{1}{2}t_n^2 | ||
| + | \end{array} \right] | ||
| + | }_{A} | ||
| + | \underbrace{ | ||
| + | \left( g \right) | ||
| + | }_{\phi} | ||
| + | = | ||
| + | \underbrace{ | ||
| + | \left( \begin{array}{c} | ||
| + | h_1-h_0 \\ h_2-h_0 \\ \vdots \\ h_n-h_0 | ||
| + | \end{array} \right) | ||
| + | }_{b} | ||
| + | </math> | ||
| + | </li> | ||
| + | |||
| + | <li>Forming the normal equations, we have <math>A^\mathsf{T}A\phi = A^\mathsf{T} b</math>, | ||
| + | :<math> | ||
| + | \left[\begin{array}{cccc} | ||
| + | \tfrac{1}{2}t_1^2 & \tfrac{1}{2}t_2^2 & \cdots & \tfrac{1}{2}t_n^2 | ||
| + | \end{array} \right] | ||
| + | \left[\begin{array}{c} | ||
| + | \tfrac{1}{2}t_1^2 \\ \tfrac{1}{2}t_2^2 \\ \vdots \\ \tfrac{1}{2}t_n^2 | ||
| + | \end{array} \right] | ||
| + | \left( g \right) | ||
| + | = | ||
| + | \left[\begin{array}{cccc} | ||
| + | \tfrac{1}{2}t_1^2 & \tfrac{1}{2}t_2^2 & \cdots & \tfrac{1}{2}t_n^2 | ||
| + | \end{array} \right] | ||
| + | \left( \begin{array}{c} | ||
| + | h_1-h_0 \\ h_2-h_0 \\ \vdots \\ h_n-h_0 | ||
| + | \end{array} \right) | ||
| + | </math> | ||
| + | </li> | ||
| + | |||
| + | <li>Using the rules of | ||
| + | [[Linear_Algebra#Matrix-Matrix_Product|matrix multiplication]], we | ||
| + | can rewrite this as | ||
| + | :<math> | ||
| + | \sum_{i=1}^n \left(\tfrac{1}{2} t_i^2 \right)^2 \cdot g = \sum_{i=1}^n \left( \tfrac{1}{2}t_i^2 \right) \left(h_i-h_0\right) | ||
| + | </math> | ||
| + | This may be easily solved for <var>g</var> | ||
| + | :<math> | ||
| + | g = 2\frac{ \sum_{i=1}^n t_i^2 \left( h_i-h_0 \right) }{ \sum_{i=1}^n t_i^4 } | ||
| + | </math> | ||
| + | </li> | ||
| + | |||
| + | <li>Substituting numbers in from our above table, we obtain '''g=-9.75 m/s<sup>2</sup>'''</li> | ||
| + | </ol> | ||
| + | |||
| + | |||
=== Converting a Nonlinear Problem Into a Linear One === | === Converting a Nonlinear Problem Into a Linear One === | ||
| + | {{Stub|section}} | ||
| + | |||
| + | |||
| + | == The R-Squared Value == | ||
| + | |||
| + | The <math>R^2</math> value is a common way to measure how well a predicted value matches the observed data. It is calculated as | ||
| + | :<math> | ||
| + | R^2 = 1 - \frac{\sum_{i=1}^{n} \left( y_{i}^{observed} - y_i^{predicted} \right)^2} | ||
| + | {\sum_{i=1}^{n} \left( y_i^{observed} - \bar{y} \right)^2 }, | ||
| + | </math> | ||
| + | where <math>y_{i}^{predicted}</math> is a predicted value of | ||
| + | <math>y</math>, <math>y_i^{observed}</math> is the observed | ||
| + | value, and <math>\bar{y}=\frac{1}{n}\sum_{i=1}^n y_i^{observed} | ||
| + | </math> is the average value of the observed value of | ||
| + | <math>y</math>. | ||
| + | |||
| + | The <math>R^2</math> value is always less than unity, <math>R^2 < 1</math>. | ||
| − | |||
== Nonlinear Least Squares Regression == | == Nonlinear Least Squares Regression == | ||
| + | |||
| + | The discussion and examples above focused on ''linear'' least squares | ||
| + | regression, where the problem could be recast as a polynomial and we | ||
| + | were solving for the coefficients of that polynomial. We showed an | ||
| + | [[#Example|example]] of the Arrhenius equation which was originally | ||
| + | nonlinear in the parameters but we rearranged it to be solved using | ||
| + | linear regression. | ||
| + | |||
| + | Occasionally, it is not possible to reduce a problem to a linear one | ||
| + | in order to perform regression. In such cases, we must use | ||
| + | ''nonlinear'' regression, which involves solving a system of nonlinear | ||
| + | equations for the unknown parameters. | ||
| + | |||
| + | |||
| + | |||
| + | === Derivation of the Linear Least Squares Equations === | ||
| + | |||
| + | |||
| + | {{Stub|section}} | ||
Latest revision as of 08:16, 26 August 2009
Contents
Introduction
Often time we measure some observable 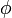 as a function
of some independent variable,
as a function
of some independent variable, 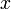 , and we have some
theoretical function that we expect the observations to obey. The
function may have parameters in it that we need to determine. The
process of determining the best values of the parameters that fit the
function to the given data is known as regression.
, and we have some
theoretical function that we expect the observations to obey. The
function may have parameters in it that we need to determine. The
process of determining the best values of the parameters that fit the
function to the given data is known as regression.
Example
Consider the Arrhenius equation commonly used to describe the rate constant in chemistry,
where
-
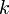 is the rate constant of the chemical reaction,
is the rate constant of the chemical reaction, -
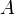 is the pre-exponential factor
is the pre-exponential factor -
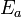 is the activation energy,
is the activation energy, -
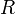 is the gas constant
is the gas constant -
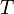 is the temperature.
is the temperature.
If we measured 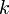 as a function of
as a function of 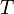 we could
determine
we could
determine 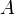 and
and 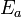 using regression.
using regression.
Linear Least Squares Regression
Linear Least Squares Regression can be applied if we can write our
function in polynomial form, 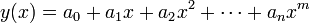 . If we can do this, then we are looking for
the coefficients of the polynomial,
. If we can do this, then we are looking for
the coefficients of the polynomial, 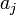 given
given
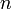 observations
observations 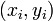 . We can write
this as
. We can write
this as
or, in matrix form,
Regression applies when 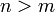 . In other words, when we have
many more equations than we have unknowns. In this case, the
least-squares solution is written as
. In other words, when we have
many more equations than we have unknowns. In this case, the
least-squares solution is written as
Example
Let's illustrate linear least squares regression with our example above. First, we must rewrite the problem:
Note that this now looks like a polynomial, 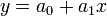 ,
where
,
where 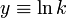 ,
, 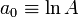 ,
,
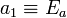 , and
, and 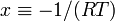 .
.
If we write these equations for each of our 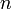 data points
in matrix form we obtain
data points
in matrix form we obtain
and the equations to be solved are
Note that since 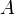 is a 2x
is a 2x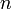 matrix and
matrix and
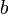 is a
is a 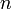 x1 vector, we have a 2x2 system of
equations to solve (see notes on
matrix multiplication).
x1 vector, we have a 2x2 system of
equations to solve (see notes on
matrix multiplication).
Example 2
Let's consider another example, where we want to determine the value
of the gravitational constant, 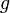 , via regression. To do
this, we could drop an object from a set height,
, via regression. To do
this, we could drop an object from a set height, 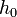 at
time
at
time 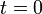 and measure its height as a function of time.
Neglecting air resistance, we have
and measure its height as a function of time.
Neglecting air resistance, we have
where 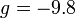 m/s2 is the gravitational
constant. Assume that
m/s2 is the gravitational
constant. Assume that 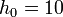 meters is known precisely,
and that since we drop the ball from rest,
meters is known precisely,
and that since we drop the ball from rest, 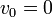 m/s. The
data we collect is given in the table below:
m/s. The
data we collect is given in the table below:
| time (s) | 0.08 | 0.28 | 0.48 | 0.53 | 0.70 | 1.05 | 1.31 | 1.36 |
| h(m) | 9.90 | 9.58 | 8.86 | 8.76 | 7.58 | 4.71 | 1.47 | 1.01 |
Let's go through this problem by hand:
- First, we rearrange our equation as follows:
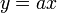 .
.
- Write down the equations in matrix form, one equation for each of
the
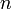 data points.
data points.
- Forming the normal equations, we have
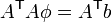 ,
,
- Using the rules of
matrix multiplication, we
can rewrite this as
- Substituting numbers in from our above table, we obtain g=-9.75 m/s2
Converting a Nonlinear Problem Into a Linear One
|
The R-Squared Value
The 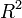 value is a common way to measure how well a predicted value matches the observed data. It is calculated as
value is a common way to measure how well a predicted value matches the observed data. It is calculated as
where 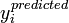 is a predicted value of
is a predicted value of
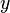 ,
, 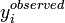 is the observed
value, and
is the observed
value, and 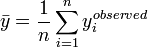 is the average value of the observed value of
is the average value of the observed value of
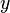 .
.
The 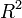 value is always less than unity,
value is always less than unity, 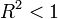 .
.
Nonlinear Least Squares Regression
The discussion and examples above focused on linear least squares regression, where the problem could be recast as a polynomial and we were solving for the coefficients of that polynomial. We showed an example of the Arrhenius equation which was originally nonlinear in the parameters but we rearranged it to be solved using linear regression.
Occasionally, it is not possible to reduce a problem to a linear one in order to perform regression. In such cases, we must use nonlinear regression, which involves solving a system of nonlinear equations for the unknown parameters.
Derivation of the Linear Least Squares Equations
|
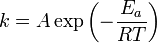
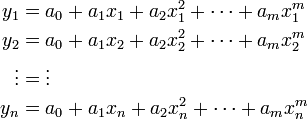
![\underbrace{ \left[ \begin{array}{ccccc}
1 & x_1 & x_1^2 & \cdots & x_1^m \\
1 & x_2 & x_2^2 & \cdots & x_2^m \\
\vdots & \vdots & \cdots & \vdots \\
1 & x_n & x_n^2 & \cdots & x_n^m
\end{array} \right] }_{A}
\underbrace{ \left( \begin{array}{c}
a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_m
\end{array}\right) }_{\phi}
=
\underbrace{ \left( \begin{array}{c}
y_1 \\ y_2 \\ \vdots \\ y_n
\end{array}\right) }_{b}](/wiki/images/math/1/7/f/17ffd709a9583bb9a1eff21ac104d0da.png)
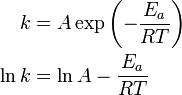
![\underbrace{ \left[ \begin{array}{cc}
1 & \frac{-1}{RT_1} \\ 1 & \frac{-1}{RT_2} \\ 1 & \frac{-1}{RT_3} \\ \vdots & \vdots \\ 1 & \frac{-1}{RT_n}
\end{array} \right] }_{A}
\underbrace{ \left(\begin{array}{c}
a_0 \\ a_1
\end{array}\right) }_{\phi}
\underbrace{ \left(\begin{array}{c}
\ln k_1 \\ \ln k_2 \\ \ln k_3 \\ \vdots \\ \ln k_n
\end{array}\right) }_{b}](/wiki/images/math/d/3/4/d34d5ee3cdd529666d7bd2e54e8293c2.png)
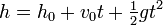
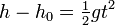
![\underbrace{
\left[\begin{array}{c}
\tfrac{1}{2}t_1^2 \\ \tfrac{1}{2}t_2^2 \\ \vdots \\ \tfrac{1}{2}t_n^2
\end{array} \right]
}_{A}
\underbrace{
\left( g \right)
}_{\phi}
=
\underbrace{
\left( \begin{array}{c}
h_1-h_0 \\ h_2-h_0 \\ \vdots \\ h_n-h_0
\end{array} \right)
}_{b}](/wiki/images/math/b/8/f/b8f1a423ad791da1da528f1be764c184.png)
![\left[\begin{array}{cccc}
\tfrac{1}{2}t_1^2 & \tfrac{1}{2}t_2^2 & \cdots & \tfrac{1}{2}t_n^2
\end{array} \right]
\left[\begin{array}{c}
\tfrac{1}{2}t_1^2 \\ \tfrac{1}{2}t_2^2 \\ \vdots \\ \tfrac{1}{2}t_n^2
\end{array} \right]
\left( g \right)
=
\left[\begin{array}{cccc}
\tfrac{1}{2}t_1^2 & \tfrac{1}{2}t_2^2 & \cdots & \tfrac{1}{2}t_n^2
\end{array} \right]
\left( \begin{array}{c}
h_1-h_0 \\ h_2-h_0 \\ \vdots \\ h_n-h_0
\end{array} \right)](/wiki/images/math/2/e/4/2e4fc204015375feffb9dd75968db57e.png)