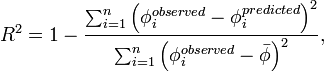Difference between revisions of "Matlab Functions"
(New page: == Why Functions? == Provide general description and motivation == Function Basics == === Arguments === === Variable Scope === == Anonymous Functions == == Calling Functions == ...) |
m (→Anonymous Functions) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | [[Category:Matlab]] | ||
| + | |||
| + | |||
== Why Functions? == | == Why Functions? == | ||
| − | + | ||
| + | Any time that you find yourself duplicating a section of code with | ||
| + | minor changes, you should consider using a function. As an example, | ||
| + | let's consider the [[Regression#The_R2_Value|R<sup>2</sup> value]], | ||
| + | commonly used in [[regression]]. | ||
| + | :<math> | ||
| + | R^2 = 1 - \frac{\sum_{i=1}^{n} \left( \phi_{i}^{observed} - \phi_i^{predicted} \right)^2} | ||
| + | {\sum_{i=1}^{n} \left( \phi_i^{observed} - \bar{\phi} \right)^2 }, | ||
| + | </math> | ||
| + | where <math>\phi_{i}^{predicted}</math> is a predicted value of | ||
| + | <math>\phi</math>, <math>\phi_i^{observed}</math> is the observed | ||
| + | value, and <math>\bar{\phi}=\frac{1}{n}\sum_{i=1}^n \phi_i^{observed} | ||
| + | </math> is the average value of the observed value of | ||
| + | <math>\phi</math>. We could create a function to calculate the | ||
| + | <math>R^2</math> value and then use it rather then repeating the code | ||
| + | to calculate <math>R^2</math> each time it is needed. | ||
| + | |||
| + | Perhaps without realizing it, you have used many functions in Matlab. | ||
| + | For example, [[Matlab_Arrays#Linspace_and_Logspace|linspace]], | ||
| + | [[Matlab_Arrays#Shortcuts_for_Special_Matrices|ones]], | ||
| + | [[Matlab_Arrays#Shortcuts_for_Special_Matrices|zeros]], etc. are all | ||
| + | functions. | ||
| + | |||
== Function Basics == | == Function Basics == | ||
| − | === | + | A function has a few basic ingredients: |
| + | * Input arguments - these are the arguments that the caller provides to the function. Functions may take 0 to many input arguments. | ||
| + | * Output arguments - these are the result(s) of the function. Functions may provide 0 to many output arguments. | ||
| + | * Documentation! See the [[#Tips_for_creating_functions|tips]] section for more information on documenting functions. | ||
| + | |||
| + | All variables used within a function can only be "seen" within that function. | ||
| + | |||
| + | |||
| + | === Example === | ||
| + | Let's consider an example of calculating the rate constant for a reaction: | ||
| + | <math>k=A \exp \left(\frac{-E_a}{RT}\right)</math> | ||
| + | A function to calculate this might look like: | ||
| + | {| border=3 cellpadding="5" cellspacing="0" | ||
| + | |+ '''rate_constant.m | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | function k = rate_constant( A, Ea, T ) | ||
| + | % k = rate_constant( A, Ea, T ) | ||
| + | % A - pre-exponential factor, units vary | ||
| + | % Ea - Activation energy, J/mol | ||
| + | |||
| + | R = 8.314; % Gas constant, J/(mol K) | ||
| + | k = A*exp(-Ea/(R*T)); | ||
| + | </source> | ||
| + | |} | ||
| + | |||
| − | |||
| + | === Tips for creating functions === | ||
| + | # The function name should be the same as the m-file that you save it in. In the above example, the function was called <tt>rate_constant</tt> and we called the matlab file <tt>rate_constant.m</tt>. | ||
| + | # Document your function! At a minimum, provide comments illustrating how to use the function and describing the input and output arguments. Then you can type "help [function]" at the command line to learn how to use it. For example, you could type <tt>help rate_constant</tt> and the first block of comments would be displayed. | ||
== Anonymous Functions == | == Anonymous Functions == | ||
| + | Occasionally we want to create a function but we don't want to hassle | ||
| + | with creating an m-file. We can use an ''anonymous function'' to help | ||
| + | here. | ||
| + | |||
| + | Anonymous functions have a few key features: | ||
| + | * They have access to any variables defined above them in the function where they are defined. | ||
| + | * They are not visible outside of the function that they are defined in. | ||
| + | |||
| + | |||
| + | As a simple example, let's assume that we want to plot | ||
| + | <math>y=x^b</math> for various values of <math>b</math>. The following | ||
| + | code does this: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | clear; clc; close all; | ||
| + | |||
| + | % create an anonymous function called "func" | ||
| + | func = @(b,x)(x.^b); | ||
| + | |||
| + | x = linspace(0.1,3,100); % independent values. | ||
| + | fx = zeros(3,100); % array to hold the function values | ||
| + | legendentry = {}; % array to stash legend entries. | ||
| + | for b=1:5 | ||
| + | % calculate the function values for this value of b | ||
| + | % and then create the legend entry. | ||
| + | fx(b,:) = func(b,x); | ||
| + | legendentry{b} = strcat('b=',num2str(b)); | ||
| + | end | ||
| + | % plot on a log-log scale | ||
| + | loglog(x,fx); | ||
| + | xlabel('x'); ylabel('x^b'); | ||
| + | legend(legendentry); | ||
| + | </source> | ||
| − | + | Of course, in this case it would have been just as easy to do this | |
| + | without a function, but this illustrates how to use an anonymous | ||
| + | function. | ||
| + | == Practical Uses of Functions == | ||
| − | + | Functions are regularly used when | |
| − | + | [[Nonlinear_equations#FZERO|solving nonlinear equations]], performing | |
| + | [[Numerical_Integration|numerical integration]], and solving | ||
| + | [[ODEs|ordinary differential equations]] in Matlab. | ||
Latest revision as of 17:03, 19 February 2009
Contents
Why Functions?
Any time that you find yourself duplicating a section of code with minor changes, you should consider using a function. As an example, let's consider the R2 value, commonly used in regression.
where 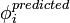 is a predicted value of
is a predicted value of
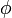 ,
, 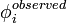 is the observed
value, and
is the observed
value, and 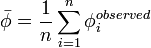 is the average value of the observed value of
is the average value of the observed value of
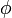 . We could create a function to calculate the
. We could create a function to calculate the
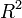 value and then use it rather then repeating the code
to calculate
value and then use it rather then repeating the code
to calculate 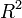 each time it is needed.
each time it is needed.
Perhaps without realizing it, you have used many functions in Matlab. For example, linspace, ones, zeros, etc. are all functions.
Function Basics
A function has a few basic ingredients:
- Input arguments - these are the arguments that the caller provides to the function. Functions may take 0 to many input arguments.
- Output arguments - these are the result(s) of the function. Functions may provide 0 to many output arguments.
- Documentation! See the tips section for more information on documenting functions.
All variables used within a function can only be "seen" within that function.
Example
Let's consider an example of calculating the rate constant for a reaction:
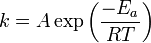 A function to calculate this might look like:
A function to calculate this might look like:
function k = rate_constant( A, Ea, T )
% k = rate_constant( A, Ea, T )
% A - pre-exponential factor, units vary
% Ea - Activation energy, J/mol
R = 8.314; % Gas constant, J/(mol K)
k = A*exp(-Ea/(R*T));
|
Tips for creating functions
- The function name should be the same as the m-file that you save it in. In the above example, the function was called rate_constant and we called the matlab file rate_constant.m.
- Document your function! At a minimum, provide comments illustrating how to use the function and describing the input and output arguments. Then you can type "help [function]" at the command line to learn how to use it. For example, you could type help rate_constant and the first block of comments would be displayed.
Anonymous Functions
Occasionally we want to create a function but we don't want to hassle with creating an m-file. We can use an anonymous function to help here.
Anonymous functions have a few key features:
- They have access to any variables defined above them in the function where they are defined.
- They are not visible outside of the function that they are defined in.
As a simple example, let's assume that we want to plot
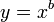 for various values of
for various values of 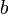 . The following
code does this:
. The following
code does this:
clear; clc; close all;
% create an anonymous function called "func"
func = @(b,x)(x.^b);
x = linspace(0.1,3,100); % independent values.
fx = zeros(3,100); % array to hold the function values
legendentry = {}; % array to stash legend entries.
for b=1:5
% calculate the function values for this value of b
% and then create the legend entry.
fx(b,:) = func(b,x);
legendentry{b} = strcat('b=',num2str(b));
end
% plot on a log-log scale
loglog(x,fx);
xlabel('x'); ylabel('x^b');
legend(legendentry);
Of course, in this case it would have been just as easy to do this without a function, but this illustrates how to use an anonymous function.
Practical Uses of Functions
Functions are regularly used when solving nonlinear equations, performing numerical integration, and solving ordinary differential equations in Matlab.