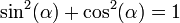Difference between revisions of "Matlab Arrays"
(→Creating Matrices) |
m |
||
| (48 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[Category:Matlab]] | [[Category:Matlab]] | ||
| + | |||
== Array Basics == | == Array Basics == | ||
| − | |||
| − | Vectors can be either a row or column vector: | + | An array is an ''n''-dimensional collection of numbers. [[Linear_Algebra#Basics: Matrices & Vectors|Matrices]] are 2-dimensional arrays, and [[Linear_Algebra#Basics: Matrices & Vectors|vectors]] are 1-dimensional arrays. |
| + | |||
| + | * '''Vectors''' can be either a row or column vector: | ||
<center> | <center> | ||
<math> | <math> | ||
\quad | \quad | ||
| − | a= | + | a= \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{bmatrix} |
\quad | \quad | ||
| − | b = | + | b = \begin{bmatrix} b_1 & b_2 & \cdots & b_n \end{bmatrix} |
\quad | \quad | ||
| − | c = | + | c = \begin{bmatrix} 1 \\ 4 \\ 3.2 \\ \pi \end{bmatrix} |
</math> | </math> | ||
</center> | </center> | ||
| − | We refer to the elements of an array by their position in the array. For example, the third element in <math>c</math> is 3.2, and the second element in <math>a</math> is <math>a_2</math>. | + | :We refer to the elements of an array by their position in the array. For example, the third element in <math>c</math> is 3.2, and the second element in <math>a</math> is <math>a_2</math>. |
| − | Matrices are two-dimensional arrays, whose elements are referred to by the ''row'' and ''column'' that they belong to. For example, | + | * '''Matrices''' are two-dimensional arrays, whose elements are referred to by the ''row'' and ''column'' that they belong to. For example, |
<center> | <center> | ||
<math> | <math> | ||
\quad | \quad | ||
| − | A = | + | A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{bmatrix} |
</math> | </math> | ||
</center> | </center> | ||
| − | is a matrix with three rows and two columns. We refer to this as a <math>\scriptstyle 3 \times 2</math> matrix. The first index | + | :is a matrix with three rows and two columns. We refer to this as a <math>\scriptstyle 3 \times 2</math> matrix. The first index refers to the row and the second index refers to the column. |
=== Transposing Arrays === | === Transposing Arrays === | ||
| Line 30: | Line 32: | ||
<center> | <center> | ||
<math> | <math> | ||
| − | A = | + | A = \begin{bmatrix} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{bmatrix} |
\quad \Rightarrow \quad | \quad \Rightarrow \quad | ||
| − | A^\mathsf{T} = | + | A^\mathsf{T} = \begin{bmatrix} 2 & 6 & 10 \\ 4 & 8 & 12 \end{bmatrix} |
</math> | </math> | ||
</center> | </center> | ||
Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | Here the <math>^\mathsf{T}</math> superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, <math>\left(A^\mathsf{T}\right)^\mathsf{T} = A</math>. | ||
| − | == Creating | + | In MATLAB, the transpose operator is given by an apostrophe, <tt>'</tt>. For example, |
| + | <source lang="matlab"> | ||
| + | A = [2 4; 6 8; 10 12 ]; % create the "A" matrix. | ||
| + | Atrans = A'; % create a new matrix holding the transpose of "A" | ||
| + | </source> | ||
| + | The first line of code here [[#Manual_Creation|creates the matrix]] and the second stores its transpose. | ||
| + | |||
| + | == Creating Arrays in Matlab == | ||
| + | In this section we will discuss several ways of creating arrays (matrices and vectors) in MATLAB. | ||
| + | |||
| + | === Manual Creation === | ||
| − | + | Often we need to create small arrays with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. The following table illustrates how to create vectors in Matlab. | |
| − | Often we need to create small | + | |
| − | <math> | + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" |
| − | a = \left[ \begin{ | + | ! Vector type !! Example !! Matlab Code |
| − | </math> | + | |- |
| − | + | | Column vector | |
| − | + | || <math> | |
| − | + | a = \left[\begin{smallmatrix} 2 \\ 4 \\ 6 \\ 8 \end{smallmatrix} \right] | |
| − | + | </math> | |
| − | + | ||<source lang="matlab"> | |
| − | + | a = [ 2; 4; 6; 8; ]; % create a column vector | |
| − | + | a = [ 2 4 6 8 ]'; % create a row vector and then | |
| − | + | % transpose it to produce a column vector. | |
| − | + | a = [ 2 | |
| + | 4 | ||
| + | 6 | ||
| + | 8 ]; % creates a column vector. | ||
| + | </source> | ||
| + | |- | ||
| + | | Row vector | ||
| + | || <math> b = \left[ \begin{smallmatrix} 1 & 3 & 5 & 7 \end{smallmatrix} \right] </math> | ||
| + | ||<source lang="matlab"> | ||
b = [ 1 3 5 7 ]; | b = [ 1 3 5 7 ]; | ||
b = [ 1, 3, 5, 7 ]; | b = [ 1, 3, 5, 7 ]; | ||
b = [ 1; 3; 5; 7 ]'; % transpose a column vector. | b = [ 1; 3; 5; 7 ]'; % transpose a column vector. | ||
| + | </source> | ||
| + | |} | ||
| − | Note that the semicolon (;) | + | Note that the semicolon (;) identifies the end of a row in the matrix. Commas may be used to separate columns in the matrix, but they are not necessary. |
| + | |||
| + | Matrices may be created directly in much the same way as vectors are. As an example, let's build the matrix | ||
| + | :<math> | ||
| + | A = \left[\begin{smallmatrix} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{smallmatrix}\right]. | ||
| + | </math> | ||
| + | This may be done in several ways. | ||
| + | <source lang="matlab"> | ||
| + | A = [ 2 4; 6 8; 10 12 ]; | ||
| + | A = [ 2 4 | ||
| + | 6 8 | ||
| + | 10 12 ]; | ||
| + | </source> | ||
| + | Note that a semicolon (;) separates each row of the matrix while spaces separate each column. | ||
| + | We may also create a matrix from vectors. For example, we may construct '''A''' from its rows as follows: | ||
| + | <source lang="matlab"> | ||
| + | arow1 = [ 2 4 ]; | ||
| + | arow2 = [ 6 8 ]; | ||
| + | arow3 = [ 10 12 ]; | ||
| + | A = [ arow1; arow2; arow3 ]; | ||
| + | </source> | ||
| + | Similarly, we can build a matrix from its columns: | ||
| + | <source lang="matlab"> | ||
| + | acol1 = [2 6 10]'; | ||
| + | acol2 = [4; 8; 12]; | ||
| + | A = [ acol1 acol2 ]; | ||
| + | </source> | ||
=== Using the ":" operator to create arrays === | === Using the ":" operator to create arrays === | ||
| − | Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The ''':''' operator can help us create such arrays: | + | |
| + | Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The ''':''' operator (see [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/colon.html&http://www.mathworks.com/access/helpdesk/help/techdoc/ref/linspace.html here] for MATLAB's explanation of this) can help us create such arrays: | ||
array = lower : increment : upper; | array = lower : increment : upper; | ||
| − | This creates an array starting at | + | |
| + | This creates an array starting at <tt>lower</tt> and ending at <tt>upper</tt> with spacing of <tt>increment</tt>. You may eliminate the <tt>increment</tt> argument, in which case it defaults to 1. | ||
Examples: | Examples: | ||
| + | |||
| + | <source lang="matlab"> | ||
a = 1:5; % creates a=[ 1 2 3 4 5 ] | a = 1:5; % creates a=[ 1 2 3 4 5 ] | ||
b = 1:1:5; % creates b=[ 1 2 3 4 5 ] | b = 1:1:5; % creates b=[ 1 2 3 4 5 ] | ||
c = 1:2:7; % creates c=[ 1 3 5 7 ] | c = 1:2:7; % creates c=[ 1 3 5 7 ] | ||
d = 1:2:8; % creates d=[ 1 3 5 7 ] | d = 1:2:8; % creates d=[ 1 3 5 7 ] | ||
| − | e = 1.1:5 % creates e=[ 1.1 2. | + | e = 1.1:5 % creates e=[ 1.1 2.1 3.1 4.1 ] |
f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ] | f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ] | ||
g = 5:-1:1; % creates g=[ 5 4 3 2 1 ]; | g = 5:-1:1; % creates g=[ 5 4 3 2 1 ]; | ||
h = (1:3)'; % creates a column vector with elements 1, 2, 3. | h = (1:3)'; % creates a column vector with elements 1, 2, 3. | ||
| − | + | </source> | |
=== Linspace and Logspace === | === Linspace and Logspace === | ||
| − | |||
| − | + | Occasionally we want to create numbers that are equally spaced between two limits. We can use the [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/linspace.html&http://www.mathworks.com/access/helpdesk/help/techdoc/ref/logspace.html linspace] command to do this. | |
| − | + | ;<source lang="matlab">linspace( lo, hi, n );</source> | |
| + | : Creates a row vector with ''n'' points equally spaced between ''lo'' and ''hi''. | ||
| + | : The last argument, <tt>n</tt> is not required. If omitted, 100 points will be used. | ||
Examples: | Examples: | ||
| + | |||
| + | <source lang="matlab"> | ||
a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ] | a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ] | ||
b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ] | b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ] | ||
c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ] | c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ] | ||
d = linspace(1,5,5)'; % creates a column vector | d = linspace(1,5,5)'; % creates a column vector | ||
| + | e = linspace(1,5); % uses 100 points between 1 and 5. | ||
| + | lo=0; hi=10; | ||
| + | f = linspace(lo,hi); % uses 100 points between lo (0) and hi (10) | ||
| + | </source> | ||
| − | Sometimes we want points logarithmically spaced. For example, we may want to create a vector a=[ 0.1 1 10 100]. | + | Sometimes we want points logarithmically spaced. For example, we may want to create a vector <tt>a=[ 0.1 1 10 100]</tt>. |
| − | + | This can be accomplished using the [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/logspace.html logspace] command: | |
| − | + | ||
| + | ; <source lang="matlab">logspace( lo, hi, n );</source> | ||
| + | : Creates a vector with ''n'' points spaced logarithmically between <math>10^\mathrm{lo}</math> and <math>10^\mathrm{hi}</math> | ||
| + | : The last argument, <tt>n</tt> is not required. If omitted, 50 points will be used. | ||
Examples: | Examples: | ||
| + | <source lang="matlab"> | ||
a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ] | a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ] | ||
b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ] | b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ] | ||
| − | c = logspace(-1,3,5)'; | + | c = logspace(-1,3,5)'; % creates a column vector |
| + | d = logspace(-3,3); % 50 points between 10^-3 and 10^3. | ||
| + | </source> | ||
| − | == | + | === Shortcuts for Special Matrices === |
| − | = | + | <source lang="matlab">ones(nrow,ncol)</source> |
| − | + | : creates an array of all ones with <tt>nrow</tt> rows and <tt>ncol</tt> columns. [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/ones.html&http://www.mathworks.com/access/helpdesk/help/techdoc/learn_matlab/f2-644.html] | |
| − | + | <source lang="matlab">zeros(nrow,ncol)</source> | |
| − | + | : creates an array of all zeros with <tt>nrow</tt> rows and <tt>ncol</tt> columns. [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/zeros.html&http://www.mathworks.com/access/helpdesk/help/techdoc/learn_matlab/f2-644.html] | |
| − | |||
| − | |||
| − | |||
| − | + | <source lang="matlab">eye(nrow,ncol)</source> | |
| − | + | : creates an array with ones on its diagonal and zeros elsewhere. [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/zeros.html&http://www.mathworks.com/access/helpdesk/help/techdoc/learn_matlab/f2-644.html] | |
| − | + | {|border="1" cellpadding="5" cellspacing="0" align="center" | |
| − | + | |+ Examples of creating matrices. | |
| − | + | |- | |
| + | ! Matlab code !! Resulting array | ||
| + | |- | ||
| + | | <source lang="matlab">eye(3,2)</source> | ||
| + | || <math>\left[\begin{smallmatrix} | ||
| + | 1 & 0 \\ | ||
| + | 0 & 1 \\ | ||
| + | 0 & 0 | ||
| + | \end{smallmatrix}\right]</math> | ||
| + | |- | ||
| + | | <source lang="matlab">eye(3,3)</source> | ||
| + | || <math>\left[\begin{smallmatrix} | ||
| + | 1 & 0 & 0 \\ | ||
| + | 0 & 1 & 0\\ | ||
| + | 0 & 0 & 1 | ||
| + | \end{smallmatrix} \right] </math> | ||
| + | |} | ||
| − | + | <source lang="matlab">rand(nrow,ncol)</source> | |
| − | + | : creates an array with <tt>nrow</tt> rows and <tt>ncol</tt> columns full of random numbers. [http://www.mathworks.com/access/helpdesk/help/techdoc/index.html?/access/helpdesk/help/techdoc/ref/rand.html&http://www.mathworks.com/access/helpdesk/help/techdoc/learn_matlab/f2-644.html] | |
| − | |||
| − | |||
| + | For more information on creating matrices, type '''help elmat''' in the command window. | ||
=== Sparse Matrices === | === Sparse Matrices === | ||
| + | |||
| + | {{Stub|section}} | ||
| + | |||
| + | |||
| + | == Array Arithmetic == | ||
| + | |||
| + | One of the most powerful features of MATLAB is the ability to perform operations on entire arrays at once. | ||
| + | |||
| + | === Addition and Subtraction === | ||
| + | |||
| + | Given two arrays '''of the same size''', one may add or subtract these as follows: | ||
| + | <source lang="matlab"> | ||
| + | C = A + B; | ||
| + | </source> | ||
| + | |||
| + | {| cellpadding="10" | ||
| + | |- valign="top" | ||
| + | | Example 1: | ||
| + | || | ||
| + | <source lang="matlab"> | ||
| + | A = rand(3); % A is 3x3 with random entries | ||
| + | B = ones(3); % B is 3x3 with 1 everywhere | ||
| + | C = A+B; % C is 3x3 formed by adding corresponding elements of A & B | ||
| + | D = B + eye(3); % Add 1 to each diagonal element in B | ||
| + | </source> | ||
| + | |- valign="top" | ||
| + | | Example 2: | ||
| + | ||<source lang="matlab"> | ||
| + | a = [1 2 3]; % 1x3 matrix (row vector) | ||
| + | b = [4 5 6]; % 1x3 matrix (row vector) | ||
| + | c = a+b; % add a and b | ||
| + | d = a' + b'; % d is a columb vector | ||
| + | </source> | ||
| + | |- valign="top" | ||
| + | | Example 3: | ||
| + | ||<source lang="matlab"> | ||
| + | A = [1 2 3; 4 5 6]; % A is 2x3 | ||
| + | a = [-1 -2 -3]; % a is 1x3 | ||
| + | b = a + A(1,:); % add first row of A to a | ||
| + | </source> | ||
| + | |} | ||
| + | |||
| + | === Multiplication === | ||
| + | |||
| + | [[Linear_Algebra#Matrix-Matrix_Product|Multiplication of two arrays]], '''C=A*B''' requires that the number of columns in A is equal to the number of rows in B. The array '''C''' has the same number of rows as '''A''' and same number of columns as '''B'''. | ||
| + | |||
| + | {| cellpadding="10" | ||
| + | |- valign="top" | ||
| + | | Example 1 | ||
| + | ||<source lang="matlab"> | ||
| + | A = rand(3); | ||
| + | B = rand(3); | ||
| + | C = A*B; | ||
| + | </source> | ||
| + | || A, B and C are all 3x3 matrices. | ||
| + | |- valign="top" | ||
| + | | Example 2 | ||
| + | ||<source lang="matlab"> | ||
| + | A = rand(3); | ||
| + | b = rand(3,1); | ||
| + | c = A*B; | ||
| + | </source> | ||
| + | || A is a 3x3 matrix, b and c are column vectors | ||
| + | |- valign="top" | ||
| + | | Example 3 | ||
| + | ||<source lang="matlab"> | ||
| + | A = rand(3,5); | ||
| + | B = rand(5,2); | ||
| + | C = A*B; | ||
| + | </source> | ||
| + | || A is 3x5, B is 5x2 and C is 3x2 | ||
| + | |} | ||
| + | |||
| + | |||
| + | === Elemental Operations === | ||
| + | |||
| + | The following table summarizes the elemental operators available in MATLAB. Each of these operators is discussed in more detail below. | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| + | |+ '''Summary of Elemental Operations''' | ||
| + | |- | ||
| + | ! Operator | ||
| + | ! Description | ||
| + | |- | ||
| + | | .* | ||
| + | | [[Matlab_Arrays#Elemental Multiplication|Elemental Multiplication]] | ||
| + | |- | ||
| + | | ./ | ||
| + | | [[Matlab_Arrays#Elemental Division|Elemental Division]] | ||
| + | |- | ||
| + | | .^ | ||
| + | | [[Matlab_Arrays#Elemental Exponentiation|Elemental Exponentiation]] | ||
| + | |} | ||
| + | |||
| + | ==== Elemental Multiplication ==== | ||
| + | |||
| + | Arrays ''of the same size'' may be multiplied or divided element-by-element using the '''.*''' operator so that '''C = A .* B''' produces an array whose elements are given by <math>C_{i,j} = A_{i,j} B_{i,j}</math>. | ||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| + | ! Matlab Code !! Resulting Arrays !! Comments | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | A = [1 2; 3 4]; | ||
| + | B = [0 1; 5 2]; | ||
| + | C = A .* B | ||
| + | </source> | ||
| + | ||<math>A = \left[\begin{smallmatrix} 1 & 2 \\ 3 & 4 \end{smallmatrix}\right]</math>, | ||
| + | <math>B = \left[\begin{smallmatrix} 0 & 1 \\ 5 & 2 \end{smallmatrix}\right]</math>, | ||
| + | <math>C = \left[\begin{smallmatrix} 0 & 2 \\ 15 & 8 \end{smallmatrix}\right]</math> | ||
| + | || C is obtained by multiplying corresponding entries in A and B. | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | a = [1 2 3]; | ||
| + | b = [2; 4; 6]; | ||
| + | c = a .* b'; | ||
| + | </source> | ||
| + | ||<math>a = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}</math>, | ||
| + | <math>b = \begin{bmatrix} 2 & 4 & 6 \end{bmatrix}</math>, | ||
| + | <math>c = \begin{bmatrix} 2 & 8 & 18 \end{bmatrix}</math> | ||
| + | ||Note that elemental multiplication is very different from [[#Multiplication|array multiplication]]. For example, | ||
| + | <source lang="matlab"> | ||
| + | d = a*b; | ||
| + | e = b*a; | ||
| + | </source> | ||
| + | would produce <math>d = 24</math>, and | ||
| + | <math> | ||
| + | e = \left[\begin{smallmatrix} | ||
| + | 2 & 4 & 6 \\ | ||
| + | 4 & 8 & 12 \\ | ||
| + | 6 & 12 & 18 | ||
| + | \end{smallmatrix}\right] | ||
| + | </math>. | ||
| + | |} | ||
| + | |||
| + | If you need to brush up on this, see the tutorial on [[Linear_Algebra#Matrix & Vector Algebra|matrix multiplication]]. | ||
| + | |||
| + | ==== Elemental Division ==== | ||
| + | |||
| + | The '''. /''' operator performs elemental division on two arrays of the ''same size''. | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| + | ! Matlab Code !! Results | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | a = [ 2 4 6 ]; | ||
| + | b = [ 1 2 3 ]; | ||
| + | c = a./b; | ||
| + | d = b./a; | ||
| + | </source> | ||
| + | || <tt>c=[2 2 2]</tt> and <tt>d=[0.5 0.5 0.5]</tt>. | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | A = [1 2 6; 12 5 6]; | ||
| + | B = [2 2 -3; 6 1 -2]; | ||
| + | C = A./B; | ||
| + | D = B./A; | ||
| + | </source> | ||
| + | ||<math>C=\left[\begin{smallmatrix} | ||
| + | 0.5 & 1 & -2 \\ | ||
| + | 2 & 5 & -3 | ||
| + | \end{smallmatrix}\right]</math> | ||
| + | <math>D=\left[\begin{smallmatrix} | ||
| + | 2 & 1 & -0.5 \\ | ||
| + | 0.5 & 0.2 & -0.3333 | ||
| + | \end{smallmatrix}\right]</math> | ||
| + | |} | ||
| + | |||
| + | ==== Elemental Exponentiation ==== | ||
| + | |||
| + | ;<source lang="matlab">A .^ b</source> | ||
| + | :results in each element in <tt>A</tt> being raised to the power <tt>b</tt>. Here <tt>b</tt> must be a scalar, ''not'' a matrix or a vector. | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| + | ! Matlab Code !! Results | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | x = linspace(-pi,pi); | ||
| + | y = sin(x); | ||
| + | z = cos(x); | ||
| + | w = y.^2 + z.^2; | ||
| + | </source> | ||
| + | || All arrays are row vectors with 100 elements since <tt>x</tt> was formed this way using the [[#Linspace_and_Logspace|linspace command]]. The <tt>w</tt> array has all entries equal to 1. | ||
| + | |} | ||
| + | |||
| + | '''NOTE:''' Elemental exponentiation is very different from array exponentiation. For example: | ||
| + | <source lang="matlab"> | ||
| + | A = [1 2; 3 4]; | ||
| + | B = A.^3; | ||
| + | C = A^3; | ||
| + | </source> | ||
| + | results in | ||
| + | <math>B = \left[\begin{smallmatrix} 1 & 8 \\ 27 & 64 \end{smallmatrix}\right]</math> | ||
| + | and | ||
| + | <math>C = \left[\begin{smallmatrix} 37 & 54 \\ 81 & 118 \end{smallmatrix} \right] </math>. | ||
| + | Here we have C=A*A*A, where these are matrix-matrix multiplications. | ||
== Accessing Arrays == | == Accessing Arrays == | ||
| + | |||
| + | Often we need to access certain elements or groups of elements from an array. There are a few ways to do this. | ||
| + | |||
=== Indexing arrays === | === Indexing arrays === | ||
| + | |||
| + | Recall that an array is simply a collection of numbers. Arrays may be 1-dimensional (vectors), 2-dimensional (matrices) or even higher dimensional. Each number in an array has a unique location identified by an ''index''. Array indexing is best illustrated by example. | ||
| + | <source lang="matlab"> | ||
| + | a = 2:2:10; % creates a row vector: [2 4 6 8 10] | ||
| + | a1 = a(1); % assigns the first element of a to "a1" | ||
| + | </source> | ||
| + | We can likewise index into a matrix as: | ||
| + | <source lang="matlab"> | ||
| + | B = [ 5 2 9; 1 7 3; 2 6 0]; | ||
| + | var = B(2,3); % var = 3 (row 2, column 3) | ||
| + | </source> | ||
| + | In general for a two-dimensional array, B(i,j) refers to the i<sup>th</sup> row and j<sup>th</sup> column of B. | ||
| + | This is extensible to arrays of higher dimensions as well. | ||
| + | |||
| + | If we return to our previous example with the B matrix, we find something interesting: | ||
| + | <source lang="matlab"> | ||
| + | B = [ 5 2 9; 1 7 3; 2 6 0]; | ||
| + | b = B(5); | ||
| + | </source> | ||
| + | What should the value of b be? One might expect this to result in an error, since B is not a vector. However, this returns ''b=7''. What is happening? Matlab actually treats a matrix as a long vector, B = [ 5 2 9 1 7 3 2 6 0 ], with each row stacked next to the previous row. Therefore, B(5) says "go to the fifth entry" counted along rows. | ||
| + | |||
| + | |||
=== Slicing arrays using the ":" operator === | === Slicing arrays using the ":" operator === | ||
| + | |||
| + | Sometimes we need to grab a group of elements from an array. We can do this using the ''':''' operator For example: | ||
| + | <source lang="matlab"> | ||
| + | A = [ 1 2 3; 4 5 6; 7 8 9 ]; | ||
| + | col1 = A(:,1); % all rows, first column | ||
| + | row2 = A(2,:); % second row, all columns | ||
| + | </source> | ||
| + | Here ''':''' acts to select all elements in the row or column of A. We can grab a subset of rows or columns by the following: | ||
| + | <source lang="matlab"> | ||
| + | A = [ 1 2 3; 4 5 6; 7 8 9 ]; | ||
| + | a = A( 1:2, 2:3 ); | ||
| + | </source> | ||
| + | This takes rows 1 and 2 and columns 2 and 3 in '''A''' and creates a new array '''a'''. Now '''a''' looks like <math>a=\begin{bmatrix}2 & 3 \\ 5 & 6 \end{bmatrix}</math>. | ||
| + | |||
| + | The ''':''' operator is a very powerful tool to extract portions of an array. | ||
| + | |||
| + | |||
| + | === Information about Arrays === | ||
| + | |||
| + | ; size | ||
| + | : returns the number of rows and columns in an array. For example, | ||
| + | :: <source lang="matlab">A = [1 2 3; 4 5 6]; </source> | ||
| + | :: <source lang="matlab">[nrow,ncol] = size(A); </source> | ||
| + | : The result of this is that nrow=2 and ncol=3. | ||
| + | |||
| + | ; length | ||
| + | : returns the number of elements in a vector. Example: | ||
| + | :: <source lang="matlab">a = [1 2 3 4 3 2 1];</source> | ||
| + | :: <source lang="matlab">na = length(a);</source> | ||
| + | : Results in na=7. | ||
| + | |||
| + | ; max | ||
| + | : For a vector, max('''v''') returns the largest element in '''v'''. For matrices, max('''V''') returns a row vector whose elements contain the maximum value in each column of '''V'''. | ||
| + | |||
| + | ; min | ||
| + | : Analogous to '''max'''. | ||
| + | |||
| + | |||
| + | === Other Useful Tools === | ||
| + | |||
| + | Use MATLAB's help command to learn more about how to use these commands. | ||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:left" | ||
| + | |- | ||
| + | ! Matlab command | ||
| + | ! Summary | ||
| + | ! Example(s) | ||
| + | |- | ||
| + | | '''sum''' | ||
| + | | | ||
| + | * For a vector, sum('''v''') returns the sum of the elements of '''v'''. | ||
| + | * For matrices, sum('''V''') returns a row vector whose elements contain the sum of the columns of '''V'''. | ||
| + | | | ||
| + | <source lang="matlab"> | ||
| + | a=sum([1 2 3]); % a=6 | ||
| + | b=sum([1 2; 3 4]); % b = [4 6] | ||
| + | </source> | ||
| + | |- | ||
| + | | '''sort''' | ||
| + | | Sort an array in ascending or descending order. | ||
| + | |<source lang="matlab">sort([2 5 1]) % gives '''1 2 5'''</source> | ||
| + | |- | ||
| + | | '''any''' | ||
| + | | any(A) Evaluates to "true" if any of the elements in the array are true (nonzero). | ||
| + | | | ||
| + | <source lang="matlab"> | ||
| + | a=[1 2 3]; b=[1 3 4]; | ||
| + | r1 = any(a>b); % r1 is FALSE (equal to 0) | ||
| + | r2 = any(a==b); % r2 is TRUE (equal to 1) since a(1) is equal to b(1). | ||
| + | </source> | ||
| + | |- | ||
| + | | '''all''' | ||
| + | | Evaluates to "true" if all of the elements in the array are true (nonzero). | ||
| + | | | ||
| + | <source lang="matlab"> | ||
| + | A = [1 2; 3 4]; | ||
| + | B = [-1 1; 2 3]; | ||
| + | r1 = all(A>B); % r1 is TRUE (equal to 1) since the elements in A are | ||
| + | % all greater than their corresponding elements in B. | ||
| + | r2 = all(2*B>A); % r2 is FALSE | ||
| + | </source> | ||
| + | |- | ||
| + | | '''find''' | ||
| + | | find(A) returns the indices where A is nonzero. | ||
| + | | | ||
| + | <source lang="matlab"> | ||
| + | A = [1 5 0; 0 2 0]; | ||
| + | i = find(A(:,1)); % i=1 | ||
| + | i = find(A(:,2)); % i=[1 2]' | ||
| + | i = find(A); % i=[1 3 4]' | ||
| + | [i,j] = find(A); % i=[ 1 1 2 ]' j=[ 1 2 2 ]' | ||
| + | i = find(A>4); % i=3 | ||
| + | [i,j] = find(A<2); % i=[1 2 1 2]' j=[1 1 3 3]' | ||
| + | </source> | ||
| + | |- | ||
| + | | '''isequal''' | ||
| + | | isequal(A,B) returns true if all elements of A and B are equal, false otherwise. | ||
| + | | | ||
| + | <source lang="matlab"> | ||
| + | A = [1 2; 3 4]; | ||
| + | B = [2 4; 6 8]; | ||
| + | c = isequal(A,B); % c is FALSE | ||
| + | d = isequal(2*A,B); % d is TRUE | ||
| + | </source> | ||
| + | Here is something a bit more complex, using the fact that <math>\sin^2(\alpha)+\cos^2(\alpha) = 1</math> | ||
| + | <source lang="matlab"> | ||
| + | x = rand(5); | ||
| + | y1 = sin(x).*sin(x); | ||
| + | z1 = cos(x).*cos(x); | ||
| + | q = ones(5); | ||
| + | c = isequal(q,y1+z1); % c is TRUE | ||
| + | </source> | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | == Cell Arrays == | ||
| + | The arrays we have discussed up to this point can hold a single type of information. For example, each element of the array can hold a single number. They could also hold a text string, as long as each text string was the same length. | ||
| + | |||
| + | Cell arrays are special kinds of arrays that can hold any type of information. For example: | ||
| + | {| border="0" cellpadding="10" cellspacing="0" | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | a = { 1, 'hi there', [5 4 3] }; | ||
| + | </source> | ||
| + | |} | ||
| + | Cell arrays are built in much the same way as a normal array with one important difference: we use <tt>{</tt> and <tt>}</tt> rather than <tt>[</tt> and <tt>]</tt> to construct the array. Accessing cell arrays is also different. For example, given the cell array <tt>a</tt> defined above, we could access its elements in the following way: | ||
| + | {| border="0" cellpadding="10" cellspacing="0" | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | a{1} % refers to 1 | ||
| + | a{2} % refers to 'hi there' | ||
| + | a{3} % refers to the array [5 4 3] | ||
| + | </source> | ||
| + | |} | ||
| + | |||
| + | Cell arrays are particularly convenient when working with text strings. For example, if we wanted to create a list of chemical compounds along with their molecular weights, we could do the following: | ||
| + | {| border="0" cellpadding="10" cellspacing="0" | ||
| + | |- | ||
| + | |<source lang="matlab"> | ||
| + | names = { 'Carbon Dioxide (CO2)','Water (H2O)','Methane (CH4)' }; | ||
| + | mw = [ 44, 18, 16 ]; | ||
| + | fprintf('\n Compound Molecular Weight\n'); | ||
| + | fprintf(' Name (g/mol)\n'); | ||
| + | fprintf('-----------------------------------\n'); | ||
| + | for i=1:length(mw) | ||
| + | fprintf('%20s %3.1f\n',names{i},mw(i)); | ||
| + | end | ||
| + | fprintf('-----------------------------------\n'); | ||
| + | </source> | ||
| + | |width="200pt"| Note: follow these links for help on [[Matlab_Loops#For_Loops|for loops]] and [[Matlab_IO|fprintf]] | ||
| + | |} | ||
Latest revision as of 08:13, 26 August 2009
Contents
Array Basics
An array is an n-dimensional collection of numbers. Matrices are 2-dimensional arrays, and vectors are 1-dimensional arrays.
- Vectors can be either a row or column vector:
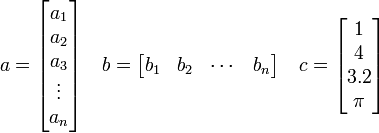
- We refer to the elements of an array by their position in the array. For example, the third element in
 is 3.2, and the second element in
is 3.2, and the second element in 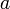 is
is 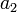 .
.
- Matrices are two-dimensional arrays, whose elements are referred to by the row and column that they belong to. For example,
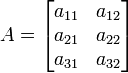
- is a matrix with three rows and two columns. We refer to this as a
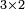 matrix. The first index refers to the row and the second index refers to the column.
matrix. The first index refers to the row and the second index refers to the column.
Transposing Arrays
Occasionally we want to transpose an array. This is done by exchanging rows and columns. For example,
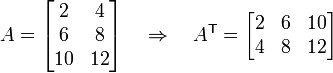
Here the 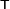 superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words,
superscript indicates transpose. Note that if we transpose an array twice, we recover the original array. In other words, 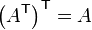 .
.
In MATLAB, the transpose operator is given by an apostrophe, '. For example,
A = [2 4; 6 8; 10 12 ]; % create the "A" matrix.
Atrans = A'; % create a new matrix holding the transpose of "A"
The first line of code here creates the matrix and the second stores its transpose.
Creating Arrays in Matlab
In this section we will discuss several ways of creating arrays (matrices and vectors) in MATLAB.
Manual Creation
Often we need to create small arrays with only a few numbers. In this case, it is easiest to create the vector in one Matlab statement. The following table illustrates how to create vectors in Matlab.
| Vector type | Example | Matlab Code |
|---|---|---|
| Column vector | ![a = \left[\begin{smallmatrix} 2 \\ 4 \\ 6 \\ 8 \end{smallmatrix} \right]](/wiki/images/math/d/e/4/de491c525f45e158295c755de080b03b.png)
|
a = [ 2; 4; 6; 8; ]; % create a column vector
a = [ 2 4 6 8 ]'; % create a row vector and then
% transpose it to produce a column vector.
a = [ 2
4
6
8 ]; % creates a column vector.
|
| Row vector | ![b = \left[ \begin{smallmatrix} 1 & 3 & 5 & 7 \end{smallmatrix} \right]](/wiki/images/math/e/c/8/ec8394ed1fad1e8f930592c67a0be40e.png)
|
b = [ 1 3 5 7 ];
b = [ 1, 3, 5, 7 ];
b = [ 1; 3; 5; 7 ]'; % transpose a column vector.
|
Note that the semicolon (;) identifies the end of a row in the matrix. Commas may be used to separate columns in the matrix, but they are not necessary.
Matrices may be created directly in much the same way as vectors are. As an example, let's build the matrix
This may be done in several ways.
A = [ 2 4; 6 8; 10 12 ];
A = [ 2 4
6 8
10 12 ];
Note that a semicolon (;) separates each row of the matrix while spaces separate each column.
We may also create a matrix from vectors. For example, we may construct A from its rows as follows:
arow1 = [ 2 4 ];
arow2 = [ 6 8 ];
arow3 = [ 10 12 ];
A = [ arow1; arow2; arow3 ];
Similarly, we can build a matrix from its columns:
acol1 = [2 6 10]';
acol2 = [4; 8; 12];
A = [ acol1 acol2 ];
Using the ":" operator to create arrays
Sometimes we have vectors that have specific patterns. For example, a=[1 2 3 4 5]. The : operator (see here for MATLAB's explanation of this) can help us create such arrays:
array = lower : increment : upper;
This creates an array starting at lower and ending at upper with spacing of increment. You may eliminate the increment argument, in which case it defaults to 1.
Examples:
a = 1:5; % creates a=[ 1 2 3 4 5 ]
b = 1:1:5; % creates b=[ 1 2 3 4 5 ]
c = 1:2:7; % creates c=[ 1 3 5 7 ]
d = 1:2:8; % creates d=[ 1 3 5 7 ]
e = 1.1:5 % creates e=[ 1.1 2.1 3.1 4.1 ]
f = 0.1:0.1:0.5 % creates f=[ 0.1 0.2 0.3 0.4 0.5 ]
g = 5:-1:1; % creates g=[ 5 4 3 2 1 ];
h = (1:3)'; % creates a column vector with elements 1, 2, 3.
Linspace and Logspace
Occasionally we want to create numbers that are equally spaced between two limits. We can use the linspace command to do this.
linspace( lo, hi, n );
- Creates a row vector with n points equally spaced between lo and hi.
- The last argument, n is not required. If omitted, 100 points will be used.
Examples:
a = linspace(1,5,5); % creates a=[ 1 2 3 4 5 ]
b = linspace(1,5,4); % creates b=[ 1.0 2.333 3.667 5.0 ]
c = linspace(5,1,5); % creates c=[ 5 4 3 2 1 ]
d = linspace(1,5,5)'; % creates a column vector
e = linspace(1,5); % uses 100 points between 1 and 5.
lo=0; hi=10;
f = linspace(lo,hi); % uses 100 points between lo (0) and hi (10)
Sometimes we want points logarithmically spaced. For example, we may want to create a vector a=[ 0.1 1 10 100]. This can be accomplished using the logspace command:
-
logspace( lo, hi, n );
- Creates a vector with n points spaced logarithmically between
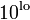 and
and 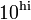
- The last argument, n is not required. If omitted, 50 points will be used.
Examples:
a = logspace(-1,3,5); % creates a=[ 0.1 1 10 100 1000 ]
b = logspace(3,-1,5); % creates b=[ 1000 100 10 1 0.1 ]
c = logspace(-1,3,5)'; % creates a column vector
d = logspace(-3,3); % 50 points between 10^-3 and 10^3.
Shortcuts for Special Matrices
ones(nrow,ncol)
- creates an array of all ones with nrow rows and ncol columns. [1]
zeros(nrow,ncol)
- creates an array of all zeros with nrow rows and ncol columns. [2]
eye(nrow,ncol)
- creates an array with ones on its diagonal and zeros elsewhere. [3]
| Matlab code | Resulting array |
|---|---|
eye(3,2)
|
![\left[\begin{smallmatrix}
1 & 0 \\
0 & 1 \\
0 & 0
\end{smallmatrix}\right]](/wiki/images/math/5/f/5/5f5be95475d9796271de3474197ac0c9.png)
|
eye(3,3)
|
![\left[\begin{smallmatrix}
1 & 0 & 0 \\
0 & 1 & 0\\
0 & 0 & 1
\end{smallmatrix} \right]](/wiki/images/math/4/f/5/4f5c63d99ef3a215bd0461a0a2e69cfe.png)
|
rand(nrow,ncol)
- creates an array with nrow rows and ncol columns full of random numbers. [4]
For more information on creating matrices, type help elmat in the command window.
Sparse Matrices
|
Array Arithmetic
One of the most powerful features of MATLAB is the ability to perform operations on entire arrays at once.
Addition and Subtraction
Given two arrays of the same size, one may add or subtract these as follows:
C = A + B;
| Example 1: |
A = rand(3); % A is 3x3 with random entries
B = ones(3); % B is 3x3 with 1 everywhere
C = A+B; % C is 3x3 formed by adding corresponding elements of A & B
D = B + eye(3); % Add 1 to each diagonal element in B
|
| Example 2: | a = [1 2 3]; % 1x3 matrix (row vector)
b = [4 5 6]; % 1x3 matrix (row vector)
c = a+b; % add a and b
d = a' + b'; % d is a columb vector
|
| Example 3: | A = [1 2 3; 4 5 6]; % A is 2x3
a = [-1 -2 -3]; % a is 1x3
b = a + A(1,:); % add first row of A to a
|
Multiplication
Multiplication of two arrays, C=A*B requires that the number of columns in A is equal to the number of rows in B. The array C has the same number of rows as A and same number of columns as B.
| Example 1 | A = rand(3);
B = rand(3);
C = A*B;
|
A, B and C are all 3x3 matrices. |
| Example 2 | A = rand(3);
b = rand(3,1);
c = A*B;
|
A is a 3x3 matrix, b and c are column vectors |
| Example 3 | A = rand(3,5);
B = rand(5,2);
C = A*B;
|
A is 3x5, B is 5x2 and C is 3x2 |
Elemental Operations
The following table summarizes the elemental operators available in MATLAB. Each of these operators is discussed in more detail below.
| Operator | Description |
|---|---|
| .* | Elemental Multiplication |
| ./ | Elemental Division |
| .^ | Elemental Exponentiation |
Elemental Multiplication
Arrays of the same size may be multiplied or divided element-by-element using the .* operator so that C = A .* B produces an array whose elements are given by 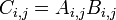 .
.
| Matlab Code | Resulting Arrays | Comments |
|---|---|---|
A = [1 2; 3 4];
B = [0 1; 5 2];
C = A .* B
|
![A = \left[\begin{smallmatrix} 1 & 2 \\ 3 & 4 \end{smallmatrix}\right]](/wiki/images/math/3/9/7/3973dc02f24b8a525d497e753d8cda15.png) , ,
|
C is obtained by multiplying corresponding entries in A and B. |
a = [1 2 3];
b = [2; 4; 6];
c = a .* b';
|
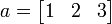 , ,
|
Note that elemental multiplication is very different from array multiplication. For example,
d = a*b;
e = b*a;
would produce |
If you need to brush up on this, see the tutorial on matrix multiplication.
Elemental Division
The . / operator performs elemental division on two arrays of the same size.
| Matlab Code | Results |
|---|---|
a = [ 2 4 6 ];
b = [ 1 2 3 ];
c = a./b;
d = b./a;
|
c=[2 2 2] and d=[0.5 0.5 0.5]. |
A = [1 2 6; 12 5 6];
B = [2 2 -3; 6 1 -2];
C = A./B;
D = B./A;
|
![C=\left[\begin{smallmatrix}
0.5 & 1 & -2 \\
2 & 5 & -3
\end{smallmatrix}\right]](/wiki/images/math/1/9/3/19364bb3ba9ec533209bb89fac5de008.png)
|
Elemental Exponentiation
A .^ b
- results in each element in A being raised to the power b. Here b must be a scalar, not a matrix or a vector.
| Matlab Code | Results |
|---|---|
x = linspace(-pi,pi);
y = sin(x);
z = cos(x);
w = y.^2 + z.^2;
|
All arrays are row vectors with 100 elements since x was formed this way using the linspace command. The w array has all entries equal to 1. |
NOTE: Elemental exponentiation is very different from array exponentiation. For example:
A = [1 2; 3 4];
B = A.^3;
C = A^3;
results in
![B = \left[\begin{smallmatrix} 1 & 8 \\ 27 & 64 \end{smallmatrix}\right]](/wiki/images/math/3/b/c/3bcfbd1c21b95f2ee3244397b0a8e308.png) and
and
![C = \left[\begin{smallmatrix} 37 & 54 \\ 81 & 118 \end{smallmatrix} \right]](/wiki/images/math/1/d/6/1d6c3ef00655b3abe64283afaa036b8b.png) .
Here we have C=A*A*A, where these are matrix-matrix multiplications.
.
Here we have C=A*A*A, where these are matrix-matrix multiplications.
Accessing Arrays
Often we need to access certain elements or groups of elements from an array. There are a few ways to do this.
Indexing arrays
Recall that an array is simply a collection of numbers. Arrays may be 1-dimensional (vectors), 2-dimensional (matrices) or even higher dimensional. Each number in an array has a unique location identified by an index. Array indexing is best illustrated by example.
a = 2:2:10; % creates a row vector: [2 4 6 8 10]
a1 = a(1); % assigns the first element of a to "a1"
We can likewise index into a matrix as:
B = [ 5 2 9; 1 7 3; 2 6 0];
var = B(2,3); % var = 3 (row 2, column 3)
In general for a two-dimensional array, B(i,j) refers to the ith row and jth column of B. This is extensible to arrays of higher dimensions as well.
If we return to our previous example with the B matrix, we find something interesting:
B = [ 5 2 9; 1 7 3; 2 6 0];
b = B(5);
What should the value of b be? One might expect this to result in an error, since B is not a vector. However, this returns b=7. What is happening? Matlab actually treats a matrix as a long vector, B = [ 5 2 9 1 7 3 2 6 0 ], with each row stacked next to the previous row. Therefore, B(5) says "go to the fifth entry" counted along rows.
Slicing arrays using the ":" operator
Sometimes we need to grab a group of elements from an array. We can do this using the : operator For example:
A = [ 1 2 3; 4 5 6; 7 8 9 ];
col1 = A(:,1); % all rows, first column
row2 = A(2,:); % second row, all columns
Here : acts to select all elements in the row or column of A. We can grab a subset of rows or columns by the following:
A = [ 1 2 3; 4 5 6; 7 8 9 ];
a = A( 1:2, 2:3 );
This takes rows 1 and 2 and columns 2 and 3 in A and creates a new array a. Now a looks like 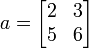 .
.
The : operator is a very powerful tool to extract portions of an array.
Information about Arrays
- size
- returns the number of rows and columns in an array. For example,
-
A = [1 2 3; 4 5 6];
-
[nrow,ncol] = size(A);
-
- The result of this is that nrow=2 and ncol=3.
- length
- returns the number of elements in a vector. Example:
-
a = [1 2 3 4 3 2 1];
-
na = length(a);
-
- Results in na=7.
- max
- For a vector, max(v) returns the largest element in v. For matrices, max(V) returns a row vector whose elements contain the maximum value in each column of V.
- min
- Analogous to max.
Other Useful Tools
Use MATLAB's help command to learn more about how to use these commands.
| Matlab command | Summary | Example(s) |
|---|---|---|
| sum |
|
a=sum([1 2 3]); % a=6
b=sum([1 2; 3 4]); % b = [4 6]
|
| sort | Sort an array in ascending or descending order. | sort([2 5 1]) % gives '''1 2 5'''
|
| any | any(A) Evaluates to "true" if any of the elements in the array are true (nonzero). |
a=[1 2 3]; b=[1 3 4];
r1 = any(a>b); % r1 is FALSE (equal to 0)
r2 = any(a==b); % r2 is TRUE (equal to 1) since a(1) is equal to b(1).
|
| all | Evaluates to "true" if all of the elements in the array are true (nonzero). |
A = [1 2; 3 4];
B = [-1 1; 2 3];
r1 = all(A>B); % r1 is TRUE (equal to 1) since the elements in A are
% all greater than their corresponding elements in B.
r2 = all(2*B>A); % r2 is FALSE
|
| find | find(A) returns the indices where A is nonzero. |
A = [1 5 0; 0 2 0];
i = find(A(:,1)); % i=1
i = find(A(:,2)); % i=[1 2]'
i = find(A); % i=[1 3 4]'
[i,j] = find(A); % i=[ 1 1 2 ]' j=[ 1 2 2 ]'
i = find(A>4); % i=3
[i,j] = find(A<2); % i=[1 2 1 2]' j=[1 1 3 3]'
|
| isequal | isequal(A,B) returns true if all elements of A and B are equal, false otherwise. |
A = [1 2; 3 4];
B = [2 4; 6 8];
c = isequal(A,B); % c is FALSE
d = isequal(2*A,B); % d is TRUE
Here is something a bit more complex, using the fact that x = rand(5);
y1 = sin(x).*sin(x);
z1 = cos(x).*cos(x);
q = ones(5);
c = isequal(q,y1+z1); % c is TRUE
|
Cell Arrays
The arrays we have discussed up to this point can hold a single type of information. For example, each element of the array can hold a single number. They could also hold a text string, as long as each text string was the same length.
Cell arrays are special kinds of arrays that can hold any type of information. For example:
a = { 1, 'hi there', [5 4 3] };
|
Cell arrays are built in much the same way as a normal array with one important difference: we use { and } rather than [ and ] to construct the array. Accessing cell arrays is also different. For example, given the cell array a defined above, we could access its elements in the following way:
a{1} % refers to 1
a{2} % refers to 'hi there'
a{3} % refers to the array [5 4 3]
|
Cell arrays are particularly convenient when working with text strings. For example, if we wanted to create a list of chemical compounds along with their molecular weights, we could do the following:
names = { 'Carbon Dioxide (CO2)','Water (H2O)','Methane (CH4)' };
mw = [ 44, 18, 16 ];
fprintf('\n Compound Molecular Weight\n');
fprintf(' Name (g/mol)\n');
fprintf('-----------------------------------\n');
for i=1:length(mw)
fprintf('%20s %3.1f\n',names{i},mw(i));
end
fprintf('-----------------------------------\n');
|
Note: follow these links for help on for loops and fprintf |
![A = \left[\begin{smallmatrix} 2 & 4 \\ 6 & 8 \\ 10 & 12 \end{smallmatrix}\right].](/wiki/images/math/9/7/e/97ef64e76a146eca2230dcaf64853a2a.png)
![B = \left[\begin{smallmatrix} 0 & 1 \\ 5 & 2 \end{smallmatrix}\right]](/wiki/images/math/f/c/1/fc184ed1b096ae4e8b96a982ae7160c1.png) ,
,
![C = \left[\begin{smallmatrix} 0 & 2 \\ 15 & 8 \end{smallmatrix}\right]](/wiki/images/math/2/c/e/2cea008e21e51bddb7ce276392ba668f.png)
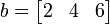 ,
,
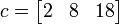
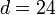 , and
, and
![e = \left[\begin{smallmatrix}
2 & 4 & 6 \\
4 & 8 & 12 \\
6 & 12 & 18
\end{smallmatrix}\right]](/wiki/images/math/c/d/9/cd9aa974b4039368ac50fb5ca4664905.png) .
.
![D=\left[\begin{smallmatrix}
2 & 1 & -0.5 \\
0.5 & 0.2 & -0.3333
\end{smallmatrix}\right]](/wiki/images/math/8/c/f/8cffb4714496fcbfbb6b578a526eca5e.png)