Difference between revisions of "Interpolation"
From Sutherland_wiki
(New page: == Linear Interpolation == == Polynomial Interpolation == == Cubic Spline Interpolation == == Lagrange Polynomial Interpolation == Given <math>n_p</math> points <math>(x_k,y_k),</ma...) |
m (→Lagrange Polynomial Interpolation) |
||
| Line 10: | Line 10: | ||
== Lagrange Polynomial Interpolation == | == Lagrange Polynomial Interpolation == | ||
| − | Given <math>n_p</math> points <math>(x_k,y_k),</math> the | + | Given <math>n_p</math> points <math>(x_k,y_k),</math> the <math>n^\mathrm{th}</math> order Lagrange polynomial that interpolates these function values, <math>f(x)</math> are expressed as |
<center> <math> f(x)=\sum_{k=0}^{n} y_{k} L_{k}(x), </math> </center> | <center> <math> f(x)=\sum_{k=0}^{n} y_{k} L_{k}(x), </math> </center> | ||
where <math>L_{k}(x)</math> is the Lagrange polynomial given by | where <math>L_{k}(x)</math> is the Lagrange polynomial given by | ||
| − | <center> <math> L_{k}(x)=\prod_{\stackrel{i=0}{i\ne k}}^{n}\frac{x-x_{i}}{x_{k}-x_{i}}. </math> </ | + | <center> <math> L_{k}(x)=\prod_{\stackrel{i=0}{i\ne k}}^{n}\frac{x-x_{i}}{x_{k}-x_{i}}, </math> </center> |
| + | and <math>n_p = n+1</math>. In other words, for an <math>n^\mathrm{th}</math> order interpolation, we require <math>n_p=n+1</math> points. | ||
| + | |||
| + | The <math>\prod</math> operator represents the continued product, and is analogous to the <math>\sum</math> operator for summations. For example, <math>\prod_{i=1}^{3} (x+i) = (x+1)(x+2)(x+3)</math>. | ||
=== Example === | === Example === | ||
Revision as of 08:42, 15 July 2008
Contents
Linear Interpolation
Polynomial Interpolation
Cubic Spline Interpolation
Lagrange Polynomial Interpolation
Given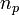 
points 
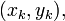the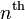 
order Lagrange polynomial that interpolates these function values, 
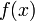are expressed as
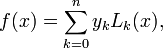
where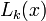 
is the Lagrange polynomial given by
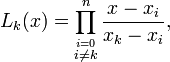
and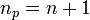 
. In other words, for an 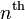order interpolation, we require 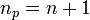points.
The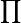 
operator represents the continued product, and is analogous to the 
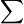operator for summations. For example, 
.
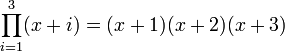