Difference between revisions of "Matlab Plotting"
m (→Histograms & Bar Graphs) |
(→Log-Scale Plots: populate this section, including an example) |
||
| Line 168: | Line 168: | ||
=== Log-Scale Plots === | === Log-Scale Plots === | ||
| − | + | Plotting things on a log-scale is useful sometimes, particularly when data spans a wide range of values from very small to very large. There are three Matlab commands that can be used to create log-scale plots: | |
| − | + | ||
| − | + | <source lang="matlab">semilogx(x,y,'abc')</source> | |
| + | : Creates a plot that is log-scale in <tt>x</tt> and linear in <tt>y</tt>. The <tt>'abc'</tt> controls [[#Basics|line formatting]]. | ||
| + | |||
| + | <source lang="matlab">semilogy(x,y,'abc')</source> | ||
| + | : Creates a plot that is linear in <tt>x</tt> and log-scale in <tt>y</tt>. | ||
| + | |||
| + | <source lang="matlab">loglog(x,y,'abc')</source> | ||
| + | : Creates a plot that is log-scale in both <tt>x</tt> and <tt>y</tt>. | ||
| + | |||
| + | ==== Example ==== | ||
| + | There is a popular saying that a piece of paper cannot be folded more than seven times [http://en.wikipedia.org/wiki/Paper_folding][http://www.abc.net.au/science/articles/2005/12/21/1523497.htm?site=science/greatmomentsinscience]. Each time you fold a piece of paper in half, the number of sheets doubles. We can express this mathematically as <math>n_s = 2^{n_f}</math>, where <math>n_s</math> is the number of sheets and <math>n_f</math> is the number of times we have folded the paper. | ||
| + | |||
| + | The thickness of the folded paper can be expressed as | ||
| + | <center><math>W = W_0 2^{n_f},</math></center> | ||
| + | where <math>W_0</math> is the thickness of a single sheet of paper. While paper comes in many thicknesses (see, [http://www.paper-paper.com/weight.html]), let's assume that a typical piece of paper is 0.004 inches (0.1 mm) thick. | ||
| + | |||
| + | Let's plot <var>W</var> as a function of the number of folds, <math>n_f</math>. The figures below show the results plotted on a linear scale (left) and semilog scale (right) | ||
| + | {|style="width:700px; background-color:LightGrey" | ||
| + | |- | ||
| + | ! linear scale on <tt>x</tt> and <tt>y</tt> (used Matlab's <tt>plot</tt> command) !! Linear scale on <tt>x</tt>, Log scale on <tt>y</tt> (used Matlab's <tt>semilogy</tt> plotting command) | ||
| + | |- | ||
| + | | [[image:paperfold_plot.png|350px]] | ||
| + | | [[image:paperfold_semilogy.png|350px]] | ||
| + | |} | ||
| + | |||
| + | The matlab file to generate these plots can be found [[media:paper_fold.m|here]]. | ||
| + | |||
| + | Note that after 20 folds, the thickness is 5243 inches (437 feet). After 30 folds, the thickness is 84.7 miles! | ||
=== Subplots === | === Subplots === | ||
Revision as of 12:15, 11 September 2008
Contents
X-Y Line Plots
Perhaps the most common plots we create as engineers are x-y line plots that show the functional dependence of one variable (y) on another (x). In MATLAB, an x-y plot is very simple to make. For example, if we want to plot 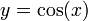 on the interval (-π,π) we can do this simply as
on the interval (-π,π) we can do this simply as
x = linspace(-pi,pi); % create the x vector
plot(x,cos(x)); % plot cos(x) versus x.
Basics
The basic syntax for plotting a function is the following
plot( x, y ); % simplest way to plot a single function
plot( x, y, 'abc'); % controls the line style
Here a represents the color to use when plotting this function, b represents the type of symbol to use (dots, squares, etc), and c represents the style of the line to use (solid, dashed, etc). The following three tables describe what to insert for a, b and c to control plot styles.
| Symbol | b | g | r | c | m | y | k | w | |
|---|---|---|---|---|---|---|---|---|---|
| Color | Blue | Green | Red | Cyan | Magenta | Yellow | Black | white | Default color |
| Symbol | . | o | x | + | * | s | d | ^ | v | < | > | p | h | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description | Point | Circle | x | plus | star | Square | Diamond | Triangle (up) | Triangle (down) | Triangle (left) | Triangle (right) | Pentagon | Hexagon | No Symbol |
| Symbol | - | : | .- | -- | |
|---|---|---|---|---|---|
| Description | Solid | Dotted | Dot-Dash | Dashed | No line |
The following are some examples of creating plots
x = linspace(-pi,pi); % create 100 points between -pi and pi
y = sin(x) .* cos(x); % evaluate a function at each point
plot(x,y,'rs:'); % plot a red dotted line with squares
figure; plot(x,y,'g--'); % plot a green dashed line
figure; plot(x,y,'ko'); % plot black circles (no line)
Note that the figure command creates a new plotting window. If you leave it out, the next plot will be overwritten.
Title and Axis Labels
Any time you create a plot, you must also label it! Axis labels (with units where appropriate) are critical. To create a title and label axes a plot in MATLAB, we use the following:
xlabel('label text');
ylabel('label text');
title('title text');
| Text | \Lambda | \Xi | \Pi | \Sigma | \Theta | \Psi | \Omega | \alpha | \beta | \gamma | \delta | \epsilon | \eta | \theta |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symbol | Λ | Ξ | Π | Σ | Θ | Ψ | Ω | α | β | γ | δ | ε | η | θ |
Example:
x=linspace(-pi,pi);
plot(x,cos(x),'r--');
xlabel('\theta');
ylabel('cos(\theta)');
title('A plot of the function cos(\theta) as a function of \theta');
Multiple Lines on a Graph
We often want to place multiple lines on a single plot. For example, if we want to plot the functions
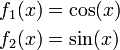
on the interval (-π,π) we could do the following
x = linspace(-pi,pi);
f1 = cos(x);
f2 = sin(x);
plot(x,f1, x,f2);
Here MATLAB automatically selects the colors for the lines. If we want more control over line styles, we can specify them ourselves:
plot(x,f1,'k-', x, f2, 'r:');
The hold on command
x = linspace(-pi,pi);
f1 = cos(x);
f2 = sin(x);
plot(x,f1,'k-');
hold on;
plot(x,f2,'r:');
hold off;
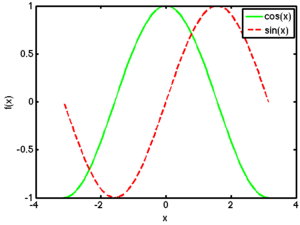
Adding a Legend
When we have multiple lines on a single plot, we should add a legend to describe each line. The legend command can be used for this purpose. Its syntax is
legend('entry 1', 'entry2', ... 'entry n');
Continuing with our previous example, we would have something like
| MATLAB Source | Resulting Plot |
|---|---|
% Manually control the line styles.
x = linspace(-pi,pi);
f1 = cos(x);
f2 = sin(x);
plot(x,f1,'g-', x, f2, 'r--');
xlabel('x'); ylabel('f(x)');
legend('cos(x)','sin(x)');
|
|
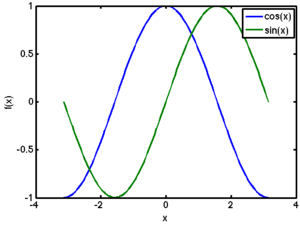
% Use MATLAB's default line styles.
x = linspace(-pi,pi);
f1 = cos(x);
f2 = sin(x);
plot(x,f1, x,f2);
xlabel('x'); ylabel('f(x)');
legend('cos(x)','sin(x)');
|
Log-Scale Plots
Plotting things on a log-scale is useful sometimes, particularly when data spans a wide range of values from very small to very large. There are three Matlab commands that can be used to create log-scale plots:
semilogx(x,y,'abc')
- Creates a plot that is log-scale in x and linear in y. The 'abc' controls line formatting.
semilogy(x,y,'abc')
- Creates a plot that is linear in x and log-scale in y.
loglog(x,y,'abc')
- Creates a plot that is log-scale in both x and y.
Example
There is a popular saying that a piece of paper cannot be folded more than seven times [1][2]. Each time you fold a piece of paper in half, the number of sheets doubles. We can express this mathematically as 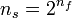 , where
, where 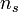 is the number of sheets and
is the number of sheets and 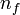 is the number of times we have folded the paper.
is the number of times we have folded the paper.
The thickness of the folded paper can be expressed as
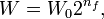
where 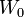 is the thickness of a single sheet of paper. While paper comes in many thicknesses (see, [3]), let's assume that a typical piece of paper is 0.004 inches (0.1 mm) thick.
is the thickness of a single sheet of paper. While paper comes in many thicknesses (see, [3]), let's assume that a typical piece of paper is 0.004 inches (0.1 mm) thick.
Let's plot W as a function of the number of folds, 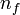 . The figures below show the results plotted on a linear scale (left) and semilog scale (right)
. The figures below show the results plotted on a linear scale (left) and semilog scale (right)
| linear scale on x and y (used Matlab's plot command) | Linear scale on x, Log scale on y (used Matlab's semilogy plotting command) |
|---|---|
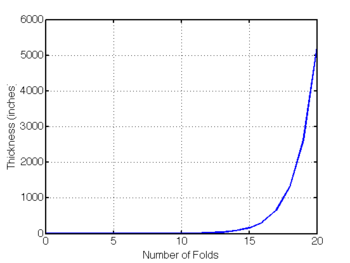
|
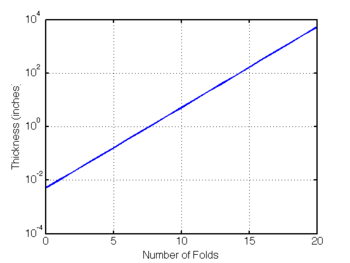
|
The matlab file to generate these plots can be found here.
Note that after 20 folds, the thickness is 5243 inches (437 feet). After 30 folds, the thickness is 84.7 miles!
Subplots
|
Fine-Tuning
- Adding a grid
- Changing axis ranges
|
Contour & Surface Plots
|
Histograms & Bar Graphs
|
Pie Charts
|