Interpolation

This page is a stub and needs to be expanded. If you can provide information or finish this page you're welcome to do so and then remove this message afterwards.

Lagrange Polynomial Interpolation

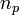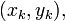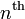Given $n_p$ points $(x_k,y_k),$ the $n^\mathrm{th}$ order Lagrange polynomial that interpolates these function values, 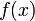$f(x)$ are expressed as

$f(x)=\sum_{k=0}^{n} y_{k} L_{k}(x),$

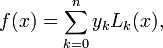
where 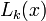$L_{k}(x)$ is the Lagrange polynomial given by

$L_{k}(x)=\prod_{\stackrel{i=0}{i\ne k}}^{n}\frac{x-x_{i}}{x_{k}-x_{i}},$

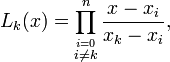
and 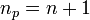$n_p = n+1$. In other words, for an 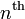$n^\mathrm{th}$ order interpolation, we require 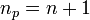$n_p=n+1$ points.

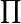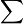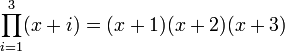The $\prod$ operator represents the continued product, and is analogous to the $\sum$ operator for summations. For example, $\prod_{i=1}^{3} (x+i) = (x+1)(x+2)(x+3)$.