Linear Systems in Matlab

Solving Linear Systems of Equations in MATLAB

$[A](x)=(b)$

See the discussion of linear algebra for help on setting up a linear system of equations. There is also help on creating matrices and vectors in MATLAB.

The simplest way of solving a system of equations in MATLAB is by using the \ operator. Given a matrix A and a vector b, we may solve the system using the following MATLAB commands

   x = A\b;

For example, if we wanted to solve the system of equations

$\begin{cases} 6y = -5x \\ y = -3x -5 \end{cases}$

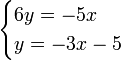
we would first rewrite these in a matrix-vector form as

$\begin{align} 5x + 6y = 0 \\ 3x + 1y &= -5 \\ \end{align} \quad \Leftrightarrow \quad \left[ \begin{array}{cc} 5 & 6 \\ 3 & 1 \end{array} \right] \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} 0 \\ -5 \end{array} \right)$

This is implemented in MATLAB as

  A = [ 5 6; 3 1 ];   % define the matrix
  b = [ 0; -5 ];      % define the vector
  solution = A\b;     % solve the system of equations.

In this example, solution is a column vector whose elements are x and y.

Note that we can also form the inverse of a matrix,

$[A] (x)=(b) \quad \Leftrightarrow \quad (x)=[A]^{-1}(b).$

This can be done in MATLAB as illustrated by the following:

  A = [ 5 6; 3 1 ];
  b = [ 0; -5 ];
  Ainv = A^-1;       % calculate the inverse of A
  solution = Ainv*b; % calculate the solution

We could also calculate A^-1 by

  Ainv = inv(A);   % entirely equivalent to A^-1.

Sparse Systems

This section is a stub and needs to be expanded. If you can provide information or finish this section you're welcome to do so and then remove this message afterwards.

Linear Systems using the Symbolic Toolbox

Occasionally we may want to find the symbolic (general) solution to a system of equations rather than a specific numerical solution. The symbolic toolbox provides a way to do this.

This section is a stub and needs to be expanded. If you can provide information or finish this section you're welcome to do so and then remove this message afterwards.