Linear Systems in Matlab

Solving Linear Systems of Equations in MATLAB

This section discusses how to solve a set of linear equations $[A](x)=(b)$ in MATLAB. See the discussion of linear algebra for help on writing a linear system of equations in matrix-vector format. There is also help on creating matrices and vectors in MATLAB.

The simplest way of solving a system of equations in MATLAB is by using the \ operator. Given a matrix A and a vector b, we may solve the system using the following MATLAB commands:

   x = A\b;  % Solve the linear system Ax=b for x.

Example

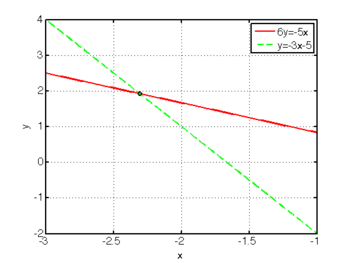
Consider the following set of equations: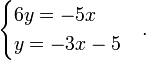

$\begin{cases} 6y = -5x \\ y = -3x -5 \end{cases}.$

These can be easily solved by hand to obtain 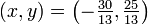$(x,y) = \left( -\tfrac{30}{13}, \tfrac{25}{13} \right)$. These equations and their solution (intersection) are plotted in the figure to the right.

To solve the system of equations using MATLAB, first rewrite these in a matrix-vector form as

$\begin{align} 5x + 6y &= 0 \\ 3x + 1y &= -5 \\ \end{align} \quad \Leftrightarrow \quad \left[ \begin{array}{cc} 5 & 6 \\ 3 & 1 \end{array} \right] \left( \begin{array}{c} x \\ y \end{array} \right) = \left( \begin{array}{c} 0 \\ -5 \end{array} \right) .$

Once in matrix-vector form, the solution is obtained in MATLAB by using the following commands (see here for help on creating matrices and vectors):

  A = [ 5 6; 3 1 ];   % define the matrix
  b = [ 0; -5 ];      % define the vector
  solution = A\b;     % solve the system of equations.

In this example, solution is a column vector whose elements are x and y:

$\mathrm{solution} = \left[ \begin{smallmatrix}-2.3077 \\1.9231 \end{smallmatrix} \right],$

which is consistent with the answer we obtained by hand above.

Matrix Inverse

Note that we can also form the inverse of a matrix,

$[A] (x)=(b) \quad \Leftrightarrow \quad (x)=[A]^{-1}(b).$

This can be done in MATLAB as illustrated by the following:

  A = [ 5 6; 3 1 ];
  b = [ 0; -5 ];
  Ainv = A^-1;       % calculate the inverse of A
  solution = Ainv*b; % calculate the solution

We could also calculate A^-1 by

  Ainv = inv(A);   % entirely equivalent to A^-1.

Sparse Systems

This section is a stub and needs to be expanded. If you can provide information or finish this section you're welcome to do so and then remove this message afterwards.

Linear Systems using the Symbolic Toolbox

Occasionally we may want to find the symbolic (general) solution to a system of equations rather than a specific numerical solution. The symbolic toolbox provides a way to do this.

This section is a stub and needs to be expanded. If you can provide information or finish this section you're welcome to do so and then remove this message afterwards.