Interpolation
From Sutherland_wiki
Contents
Linear Interpolation
Polynomial Interpolation
Cubic Spline Interpolation
Lagrange Polynomial Interpolation
Given 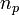 points
points 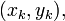 the
the 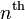 order Lagrange polynomial that interpolates these function values,
order Lagrange polynomial that interpolates these function values, 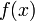 are expressed as
are expressed as
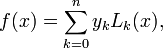
where 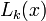 is the Lagrange polynomial given by
is the Lagrange polynomial given by
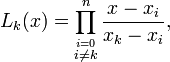
and 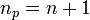 . In other words, for an
. In other words, for an 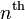 order interpolation, we require
order interpolation, we require 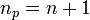 points.
points.
The 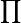 operator represents the continued product, and is analogous to the
operator represents the continued product, and is analogous to the 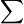 operator for summations. For example,
operator for summations. For example, 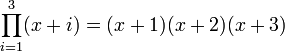 .
.