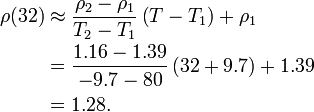Difference between revisions of "Interpolation"
m (→Lagrange Polynomial Interpolation) |
|||
| Line 167: | Line 167: | ||
== Lagrange Polynomial Interpolation == | == Lagrange Polynomial Interpolation == | ||
| + | {{Stub|section}} | ||
Given <math>n_p</math> points <math>(x_k,y_k),</math> the <math>n^\mathrm{th}</math> order Lagrange polynomial that interpolates these function values, <math>f(x)</math> are expressed as | Given <math>n_p</math> points <math>(x_k,y_k),</math> the <math>n^\mathrm{th}</math> order Lagrange polynomial that interpolates these function values, <math>f(x)</math> are expressed as | ||
Revision as of 15:10, 1 September 2008
Contents
Linear Interpolation
A linear function may be written as
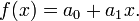 Given any two data points,
Given any two data points, 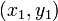 , and
, and 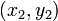 , we can determine a linear function that exactly passes through these points. We can do this by solving for
, we can determine a linear function that exactly passes through these points. We can do this by solving for 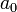 and
and 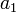 . Since there are two unknowns we require two equations. They are:
. Since there are two unknowns we require two equations. They are:
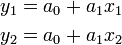
These may be written in matrix form as
![\left[ \begin{array}{cc} 1 & x_1 \\ 1 & x_2 \end{array} \right]
\left( \begin{array}{c} a_0 \\ a_1 \end{array} \right)
=
\left( \begin{array}{c} y_1 \\ y_2 \end{array} \right)](/wiki/images/math/8/9/d/89d586401931241c16145d9dbb27201a.png)
Given values for 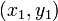 , and
, and 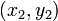 , these equations may be easily solved in MATLAB. But since they are so simple, we can easily by hand to obtain a general solution,
, these equations may be easily solved in MATLAB. But since they are so simple, we can easily by hand to obtain a general solution,
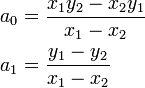
This gives the coefficients, which may then be substituted into the original equation 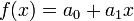 and simplified to obtain
and simplified to obtain
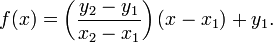
This is a very convenient equation for performing linear interpolation.
Example
The density of air at various temperatures and atmospheric pressure is given in the following table
| Temperature (°F) | 1.39 | 1.16 | 0.99 | 0.87 | 0.78 | 0.69 | 0.63 | 0.58 | 0.54 | 0.50 | 0.46 | 0.44 | 0.41 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Density (kg/m3) | -10 | 80 | 170 | 260 | 350 | 440 | 530 | 620 | 710 | 800 | 890 | 980 | 1070 |
Estimate the density of air at 32 °F. Using linear interpolation, we have 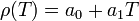 .
We define
.
We define 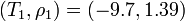 and
and 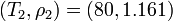 . Now we can calculate
. Now we can calculate
Implementation in Matlab
There are three ways to do interpolation in MATLAB.
- Solve the linear system.
T1=-9.7; T2=80; rho1=1.39; rho2=1.16; T = 32; A = [ 1 T1; 1 T2 ]; b = [ rho1; rho2 ]; a = A\b; rho = a(1) + a(2)*T;
- Use the general equation we derived above:
T1=-9.7; T2-80; rho1=1.39; rho2=1.16; T = 32; rho = (rho2-rho1)/(T2-T1) * (T-T1) + rho1;
- Use MATLAB's built-in interpolation tool
Ti = [-9.7 80]; rhoi = [1.39 1.16]; rho = interp1( Ti, rhoi, 32 );
All three of these methods provide exactly the same answer. However, using MATLAB's interp1 function allows you to use a vector for the points that you want to interpolate to. For example, if we wanted the density at 30, 50, 70, 10, and 110 °F, we could accomplish this by:
Ti = [-9.7 80 170 ];
rhoi = [1.39 1.16 0.995];
T = 30:20:110;
rho = interp1( Ti, rhoi, T );
Implementation in Excel
{{Stub}|section}}
Polynomial Interpolation
Polynomial interpolation is a simple extension of linear interpolation. In general, an nth degree polynomial is given as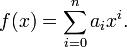
If n=1 then we recover a first-degree polynomial, which is linear. The formula gives 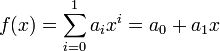 .
.
In general, if we want to interpolate a set of data using an nth degree polynomial, then we must determine n+1 coefficients,  . Therefore, we require n+1 points to interpolate using an nth degree polynomial.
. Therefore, we require n+1 points to interpolate using an nth degree polynomial.
The equations that must be solved are given as
![\left[\begin{array}{ccccc}
1 & x_{1} & x_{1}^2 & \cdots & x_{1}^{n}\\
1 & x_{2} & x_{2}^2 & \cdots & x_{2}^{n}\\
\vdots & \vdots & \vdots & \cdots & \vdots \\
1 & x_{n+1} & x_{n+1}^2 & \cdots & x_{n+1}^{n}\end{array}\right]\left(\begin{array}{c}
a_{0}\\
a_{1}\\
\vdots\\
a_{n}\end{array}\right)
=
\left(\begin{array}{c}
y_{1}\\
y_{2}\\
\vdots\\
y_{n+1}\end{array}\right)](/wiki/images/math/5/d/e/5dec415feed2a5970262778546fd8a82.png)
Solving these equations provides the values for the coefficients,  . Once we know these coefficients, we can evaluate the polynomial at any point.
. Once we know these coefficients, we can evaluate the polynomial at any point.
Example
Using a third degree polynomial, approximate the density of air at the following temperatures: 50, 300, 500 °F.
We require 4 points to fit a third degree polynomial,  . We will choose the 4 points closest to the temperature that we wish to interpolate to.
. We will choose the 4 points closest to the temperature that we wish to interpolate to.
Implementation in Matlab
Our procedure is:
- Determine which points we need to use.
- Set up and solve the linear system to obtain the polynomial coefficients
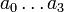 .
. - Evaluate the polynomial to obtain the temperature.
Ti = [ -9.7 80 170 260 350 440 530 620 710 800 890 980 1070 ]';
rhoi=[ 1.39 1.16 0.99 0.87 0.78 0.69 0.63 0.58 0.54 0.50 0.46 0.44 0.41 ]';
T = 50;
points = 1:4;
A = [ ones(4,1), ones(4,1).*Ti(points), ones(4,1)*Ti(points).^2, ones(4,1)*Ti(points).^3 ];
b = rhoi(points);
a = A\b;
rho = a(0) + a(1)*T + a(2)*T^2 + a(3)*T^3;
For T=300 we would repeat the above with the only change being:
T=300;
points=4:8;
For T=500 we would change
T=500;
points=5:9;
Cubic Spline Interpolation
|
Example
Implementation in Matlab
Lagrange Polynomial Interpolation
|
Given 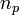 points
points 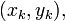 the
the 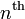 order Lagrange polynomial that interpolates these function values,
order Lagrange polynomial that interpolates these function values, 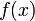 are expressed as
are expressed as
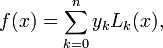
where 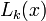 is the Lagrange polynomial given by
is the Lagrange polynomial given by
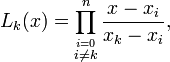
and 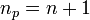 . In other words, for an
. In other words, for an 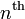 order interpolation, we require
order interpolation, we require 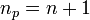 points.
points.
The 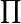 operator represents the continued product, and is analogous to the
operator represents the continued product, and is analogous to the 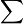 operator for summations. For example,
operator for summations. For example, 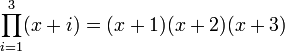 .
.