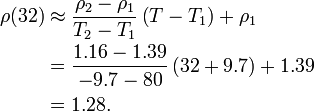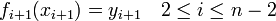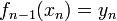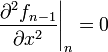Difference between revisions of "Interpolation"
(→Example) |
(Add description of cubic spline interpolation) |
||
| Line 172: | Line 172: | ||
points=4:8; | points=4:8; | ||
</source></ul> | </source></ul> | ||
| + | |||
| + | |||
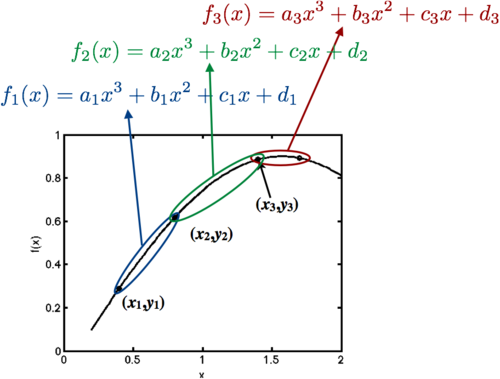
== Cubic Spline Interpolation == | == Cubic Spline Interpolation == | ||
| − | {{ | + | Cubic spline interpolation uses cubic polynomials to interpolate datasets. The concept is illustrated in the following figure: |
| + | [[image:spline1.png|center|500px]] | ||
| + | |||
| + | The data points are connected with cubic functions, and on each interval the coefficients must be determined. If we have <math>n</math> data points then we can define <math>n-1</math> cubic functions, one between each data point. For each spline we have four coefficients to determine. Therefore, we require <math>4(n-1)</math> constraints to determine the <math>4(n-1)</math> coefficients. | ||
| + | |||
| + | The constraints may be summarized in the following table: | ||
| + | |||
| + | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:center" | ||
| + | |+ Constraints for Cubic Splines | ||
| + | |- | ||
| + | ! width="375"|Description | ||
| + | ! Mathematical Statement | ||
| + | ! Number of Constraints | ||
| + | |- valign="top" | ||
| + | | At each data point, two splines meet. Here the splines must be equal to the data values. | ||
| + | | <math>f_{i}(x_{i+1}) = y_{i+1} \quad 2 \le i \le n-2</math> | ||
| + | <math>f_{i+1}(x_{i+1}) = y_{i+1} \quad 2 \le i \le n-2</math> | ||
| + | | <math>2(n-2)</math> | ||
| + | |- valign="top" | ||
| + | | At the first and last point, the function must equal the data. | ||
| + | | <math>f_1(x_1) = y_1</math> | ||
| + | <math>f_{n-1}(x_n)=y_n</math> | ||
| + | | <math>2</math> | ||
| + | |- valign="top" | ||
| + | | At each interior point the first derivatives of adjacent splines must be equivalent. | ||
| + | | <math>\left. \frac{\partial f_{i}}{\partial x} \right|_{i+1} = \left. \frac{\partial f_{i+1}}{\partial x} \right|_{i+1}</math> | ||
| + | | <math>n-2</math> | ||
| + | |- valign="top" | ||
| + | | At each interior point, the second derivatives of adjacent splines must be equivalent. | ||
| + | | <math>\left. \frac{\partial^2 f_{i}}{\partial x^2} \right|_{i+1} = \left. \frac{\partial^2 f_{i+1}}{\partial x^2} \right|_{i+1}</math> | ||
| + | | <math>n-2</math> | ||
| + | |- valign="top" | ||
| + | | We specify the curvature at the end points. By choosing the curvature to be equal to zero, we obtain a natural spline. | ||
| + | | <math>\left. \frac{\partial^2 f_1}{\partial x^2} \right|_{1} = 0</math> | ||
| + | <math>\left. \frac{\partial^2 f_{n-1}}{\partial x^2} \right|_{n} = 0</math> | ||
| + | | <math>2</math> | ||
| + | |} | ||
| + | |||
| + | Adding up all of the constraints, we see that we have <math>4(n-1)</math> constraints - precisely the number that we need. We could formulate equations for all of these constraints and solve them all to determine the coefficients for the cubic function on each interval. | ||
| + | <br clear="all" /> | ||
=== Example === | === Example === | ||
| + | Using the data in the table above, determine the density of air at the following temperatures: 60, 120, 180, 240, 300, 360, 420, 480, 540 °F. | ||
==== Implementation in Matlab ==== | ==== Implementation in Matlab ==== | ||
| + | Matlab has built-in functions for cubic spline interpolation: | ||
| + | <source lang="matlab"> | ||
| + | y = interp1( xi, yi, x, 'spline' ); | ||
| + | </source> | ||
| + | : <tt>(xi,yi)</tt> are the points at which we have data defined. | ||
| + | : <tt>x</tt> is the point(s) where we want to interpolate. | ||
| + | : <tt>'spline'</tt> tells Matlab to interpolate using cubic splines. | ||
| + | |||
| + | Using this built-in function, we may obtain the interpolated values as follows: | ||
| + | |||
| + | <ul><source lang="matlab"> | ||
| + | % Set the data points from the table. | ||
| + | Ti = [ -9.7 80 170 260 350 440 530 ... | ||
| + | 620 710 800 890 980 1070 ]'; | ||
| + | rhoi=[ 1.39 1.16 0.99 0.87 0.78 0.69 0.63 ... | ||
| + | 0.58 0.54 0.50 0.46 0.44 0.41 ]'; | ||
| + | |||
| + | % set the temperatures that we want to interpolate to. | ||
| + | T = 60:60:540; | ||
| + | |||
| + | % determine the density at the desired temperatures. | ||
| + | rho = interp1( Ti, rhoi, T, 'spline' ); | ||
| + | </source></ul> | ||
Revision as of 17:58, 1 September 2008
Contents
Linear Interpolation
A linear function may be written as
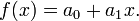 Given any two data points,
Given any two data points, 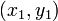 , and
, and 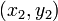 , we can determine a linear function that exactly passes through these points. We can do this by solving for
, we can determine a linear function that exactly passes through these points. We can do this by solving for 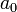 and
and 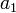 . Since there are two unknowns we require two equations. They are:
. Since there are two unknowns we require two equations. They are:
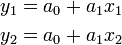
These may be written in matrix form as
![\left[ \begin{array}{cc} 1 & x_1 \\ 1 & x_2 \end{array} \right]
\left( \begin{array}{c} a_0 \\ a_1 \end{array} \right)
=
\left( \begin{array}{c} y_1 \\ y_2 \end{array} \right)](/wiki/images/math/8/9/d/89d586401931241c16145d9dbb27201a.png)
Given values for 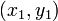 , and
, and 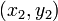 , these equations may be easily solved in MATLAB. But since they are so simple, we can easily by hand to obtain a general solution,
, these equations may be easily solved in MATLAB. But since they are so simple, we can easily by hand to obtain a general solution,
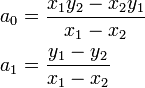
This gives the coefficients, which may then be substituted into the original equation 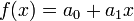 and simplified to obtain
and simplified to obtain
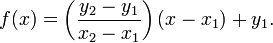
This is a very convenient equation for performing linear interpolation.
Example
The density of air at various temperatures and atmospheric pressure is given in the following table
| Temperature (°F) | 1.39 | 1.16 | 0.99 | 0.87 | 0.78 | 0.69 | 0.63 | 0.58 | 0.54 | 0.50 | 0.46 | 0.44 | 0.41 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Density (kg/m3) | -10 | 80 | 170 | 260 | 350 | 440 | 530 | 620 | 710 | 800 | 890 | 980 | 1070 |
Estimate the density of air at 32 °F. Using linear interpolation, we have 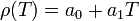 .
We define
.
We define 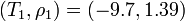 and
and 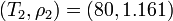 . Now we can calculate
. Now we can calculate
Implementation in Matlab
There are three ways to do interpolation in MATLAB.
- Solve the linear system.
T1=-9.7; T2=80; rho1=1.39; rho2=1.16; T = 32; A = [ 1 T1; 1 T2 ]; b = [ rho1; rho2 ]; a = A\b; rho = a(1) + a(2)*T;
- Use the general equation we derived above:
T1=-9.7; T2-80; rho1=1.39; rho2=1.16; T = 32; rho = (rho2-rho1)/(T2-T1) * (T-T1) + rho1;
- Use MATLAB's built-in interpolation tool
Ti = [-9.7 80]; rhoi = [1.39 1.16]; rho = interp1( Ti, rhoi, 32 );
All three of these methods provide exactly the same answer. However, using MATLAB's interp1 function allows you to use a vector for the points that you want to interpolate to. For example, if we wanted the density at 30, 50, 70, 10, and 110 °F, we could accomplish this by:
Ti = [-9.7 80 170 ];
rhoi = [1.39 1.16 0.995];
T = 30:20:110;
rho = interp1( Ti, rhoi, T );
Implementation in Excel
|
Polynomial Interpolation
Polynomial interpolation is a simple extension of linear interpolation. In general, an nth degree polynomial is given as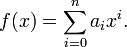
If n=1 then we recover a first-degree polynomial, which is linear. The formula gives 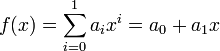 .
.
In general, if we want to interpolate a set of data using an nth degree polynomial, then we must determine n+1 coefficients, 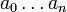 . Therefore, we require n+1 points to interpolate using an nth degree polynomial.
. Therefore, we require n+1 points to interpolate using an nth degree polynomial.
The equations that must be solved are given as
![\left[\begin{array}{ccccc}
1 & x_{1} & x_{1}^2 & \cdots & x_{1}^{n}\\
1 & x_{2} & x_{2}^2 & \cdots & x_{2}^{n}\\
\vdots & \vdots & \vdots & \cdots & \vdots \\
1 & x_{n+1} & x_{n+1}^2 & \cdots & x_{n+1}^{n}\end{array}\right]\left(\begin{array}{c}
a_{0}\\
a_{1}\\
\vdots\\
a_{n}\end{array}\right)
=
\left(\begin{array}{c}
y_{1}\\
y_{2}\\
\vdots\\
y_{n+1}\end{array}\right)](/wiki/images/math/5/d/e/5dec415feed2a5970262778546fd8a82.png)
Solving these equations provides the values for the coefficients, 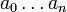 . Once we know these coefficients, we can evaluate the polynomial at any point.
. Once we know these coefficients, we can evaluate the polynomial at any point.
Example
Using a third degree polynomial and the data in the table above, approximate the density of air at 50 °F and 300 °F.
We require 4 points to fit a third degree polynomial, 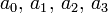 . The equations to be solved are:
. The equations to be solved are:
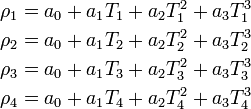
Once we have solved these equations we have the polynomial coefficients and we can then evaluate the resulting polynomial at any temperature that we wish.
We still must choose what 4 points in the table to use in the above equations. We will choose the 4 points in the table that are closest to the temperature that we wish to interpolate to. Note that if we want to evaluate the density at different temperatures, we may want to use different points in the table to determine the coefficients!
Our procedure to perform the interpolation is:
- Determine which points we need to use.
- Set up and solve the linear system to obtain the polynomial coefficients
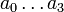 .
. - Evaluate the polynomial to obtain the temperature.
Implementation in Matlab
The MATLAB code to obtain the density at 50 °F is
% Set the data points from the table.
Ti = [ -9.7 80 170 260 350 440 530 ...
620 710 800 890 980 1070 ]';
rhoi=[ 1.39 1.16 0.99 0.87 0.78 0.69 0.63 ...
0.58 0.54 0.50 0.46 0.44 0.41 ]';
% Set the temperature we want to evaluate the density at.
T = 50;
% determine the set of points that we will use to construct
% the interpolant. We want to use points that are closest
% to the temperature that we are interested in.
points = 1:4;
% set up the linear system
A = [ ones(4,1), ones(4,1).*Ti(points), ones(4,1)*Ti(points).^2, ones(4,1)*Ti(points).^3 ];
b = rhoi(points);
% solve for the polynomial coefficients
a = A\b;
% evaluate the density.
rho = a(0) + a(1)*T + a(2)*T^2 + a(3)*T^3;
For T=300 we would probably want to choose a different set of points to determine the polynomial coefficients. Therefore, we would repeat the above with the only change being:
T=300;
points=4:8;
Cubic Spline Interpolation
Cubic spline interpolation uses cubic polynomials to interpolate datasets. The concept is illustrated in the following figure:
The data points are connected with cubic functions, and on each interval the coefficients must be determined. If we have 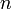 data points then we can define
data points then we can define 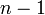 cubic functions, one between each data point. For each spline we have four coefficients to determine. Therefore, we require
cubic functions, one between each data point. For each spline we have four coefficients to determine. Therefore, we require 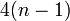 constraints to determine the
constraints to determine the 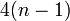 coefficients.
coefficients.
The constraints may be summarized in the following table:
| Description | Mathematical Statement | Number of Constraints |
|---|---|---|
| At each data point, two splines meet. Here the splines must be equal to the data values. | 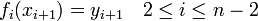
|
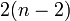
|
| At the first and last point, the function must equal the data. | 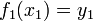
|
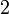
|
| At each interior point the first derivatives of adjacent splines must be equivalent. | 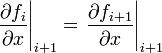
|
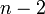
|
| At each interior point, the second derivatives of adjacent splines must be equivalent. | 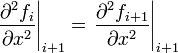
|
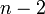
|
| We specify the curvature at the end points. By choosing the curvature to be equal to zero, we obtain a natural spline. | 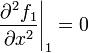
|
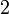
|
Adding up all of the constraints, we see that we have 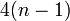 constraints - precisely the number that we need. We could formulate equations for all of these constraints and solve them all to determine the coefficients for the cubic function on each interval.
constraints - precisely the number that we need. We could formulate equations for all of these constraints and solve them all to determine the coefficients for the cubic function on each interval.
Example
Using the data in the table above, determine the density of air at the following temperatures: 60, 120, 180, 240, 300, 360, 420, 480, 540 °F.
Implementation in Matlab
Matlab has built-in functions for cubic spline interpolation:
y = interp1( xi, yi, x, 'spline' );
- (xi,yi) are the points at which we have data defined.
- x is the point(s) where we want to interpolate.
- 'spline' tells Matlab to interpolate using cubic splines.
Using this built-in function, we may obtain the interpolated values as follows:
% Set the data points from the table.
Ti = [ -9.7 80 170 260 350 440 530 ...
620 710 800 890 980 1070 ]';
rhoi=[ 1.39 1.16 0.99 0.87 0.78 0.69 0.63 ...
0.58 0.54 0.50 0.46 0.44 0.41 ]';
% set the temperatures that we want to interpolate to.
T = 60:60:540;
% determine the density at the desired temperatures.
rho = interp1( Ti, rhoi, T, 'spline' );
Lagrange Polynomial Interpolation
|
Given 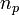 points
points 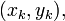 the
the 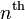 order Lagrange polynomial that interpolates these function values,
order Lagrange polynomial that interpolates these function values, 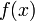 are expressed as
are expressed as
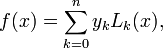
where 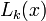 is the Lagrange polynomial given by
is the Lagrange polynomial given by
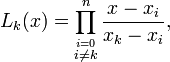
and 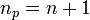 . In other words, for an
. In other words, for an 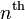 order interpolation, we require
order interpolation, we require 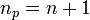 points.
points.
The 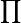 operator represents the continued product, and is analogous to the
operator represents the continued product, and is analogous to the 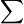 operator for summations. For example,
operator for summations. For example, 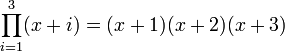 .
.