Difference between revisions of "Numerical Differentiation"
(→Lagrange Polynomials: add table of Lagrange polynomial stencils.) |
m (fix a mistake in the text on deriving the stencils from Taylor series.) |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 43: | Line 43: | ||
If we subtract the Taylor series expansion at <math>x_{i-1}</math> | If we subtract the Taylor series expansion at <math>x_{i-1}</math> | ||
| − | from the one at <math>x_{i | + | from the one at <math>x_{i+1}</math>, we find |
:<math> | :<math> | ||
f(x_{i+1})-f(x_{i-1}) = 2f^{\prime}(x_i)h + \tfrac{1}{3} f^{\prime\prime\prime}(x_i) h^3 + \cdots | f(x_{i+1})-f(x_{i-1}) = 2f^{\prime}(x_i)h + \tfrac{1}{3} f^{\prime\prime\prime}(x_i) h^3 + \cdots | ||
| Line 120: | Line 120: | ||
Lagrange polynomials, which are commonly used for [[Interpolation#Lagrange_Polynomial_Interpolation|interpolation]], can also be used for differentiation. The formula is | Lagrange polynomials, which are commonly used for [[Interpolation#Lagrange_Polynomial_Interpolation|interpolation]], can also be used for differentiation. The formula is | ||
| − | + | :<math>f^{\prime}(x) = \sum_{k=0}^n y_k L_{k}^{\prime}(x),</math> | |
where <math>L_{k}^{\prime}(x)</math> is given as | where <math>L_{k}^{\prime}(x)</math> is given as | ||
| − | + | :<math>L_{k}^{\prime}(x) = \left[ \sum_{{j=0}\atop{j\ne k}}^{n} \left( \prod_{ {i=0}\atop{i \ne j,k} }^n (x-x_i) \right) \right] \left[ \prod_{{i=0}\atop{i\ne k}}^{n} (x_k-x_i) \right]^{-1}. </math> | |
Here <math>n</math> is the order of the polynomial and we require <math>n_p=n+1</math> points to form the Lagrange polynomial. | Here <math>n</math> is the order of the polynomial and we require <math>n_p=n+1</math> points to form the Lagrange polynomial. | ||
| − | Here are the results for <var> | + | Here are the results for <var>n = 2, 3, 4</var> |
| − | {| border=1 cellpadding=10 cellspacing=1 | + | :{| border=1 cellpadding=10 cellspacing=1 |
! | ! | ||
! <var>n</var>=2 | ! <var>n</var>=2 | ||
Latest revision as of 15:56, 26 August 2010
Introduction
Often we need to approximate the derivative of a function when we cannot obtain it analytically. Here we discuss several ways to do this numerically.
Taylor Series
Let's consider the situation where we have samples of a function
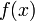 at discrete points
at discrete points 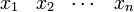 seperated by spacing
seperated by spacing
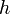 as depicted in the following figure:
as depicted in the following figure:
Consider a Taylor series expansions about some
arbitrary point 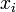 . Since
. Since 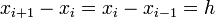 we can write these as follows:
we can write these as follows:
Approximation location Taylor Series Expansion about 
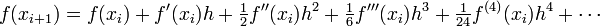
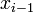
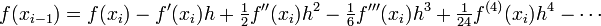
If we subtract the Taylor series expansion at 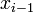 from the one at
from the one at 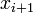 , we find
, we find
Now we solve this for 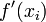 to find
to find
Now if 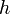 is small, then the second term (with the
is small, then the second term (with the
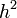 in it) is small and we can approximate the derivative
as
in it) is small and we can approximate the derivative
as
We call this a second order approximation to
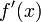 because when we truncated the series
approximation to
because when we truncated the series
approximation to 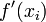 the largest term there was
of the order of
the largest term there was
of the order of 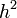 .
.
Note that we now have a way to approximate the derivative of a function if we have the function's values at two locations.
On a uniform mesh, we can use this technique to generate a variety of approximations to derivatives, as summarized in the following table:
|
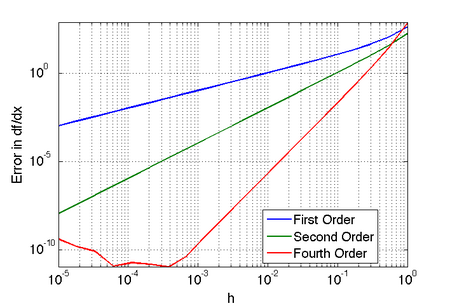 Error in approximation of 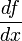 as a function of the size of the interval as a function of the size of the interval 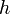 . Click here to download the matlab file that produced this plot. . Click here to download the matlab file that produced this plot. |
As can be seen in the figure above, higher order approximations result
in significantly lower error for a given spacing 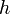 . Note
that for
. Note
that for 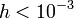 the fourth-order approximation is
contaminated by roundoff error. The same would happen for the other
derivative approximations, but at smaller
the fourth-order approximation is
contaminated by roundoff error. The same would happen for the other
derivative approximations, but at smaller 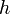 .
.
Lagrange Polynomials
Lagrange polynomials, which are commonly used for interpolation, can also be used for differentiation. The formula is
where 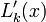 is given as
is given as
Here 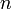 is the order of the polynomial and we require
is the order of the polynomial and we require 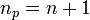 points to form the Lagrange polynomial.
points to form the Lagrange polynomial.
Here are the results for n = 2, 3, 4
n=2 n=3 n=4 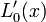
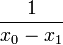
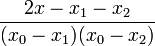
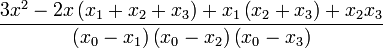
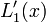
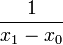
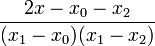
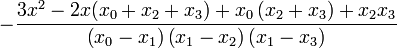
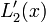
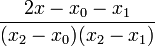
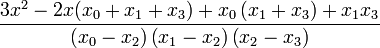
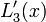
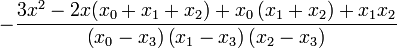
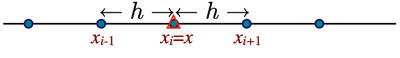
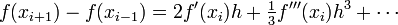
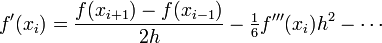
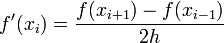
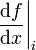
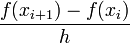
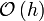
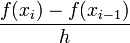
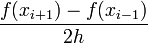
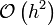
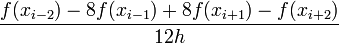
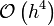
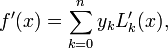
![L_{k}^{\prime}(x) = \left[ \sum_{{j=0}\atop{j\ne k}}^{n} \left( \prod_{ {i=0}\atop{i \ne j,k} }^n (x-x_i) \right) \right] \left[ \prod_{{i=0}\atop{i\ne k}}^{n} (x_k-x_i) \right]^{-1}.](/wiki/images/math/3/c/c/3cced1f629b2f0354163c2308a6df53c.png)