Difference between revisions of "Numerical Differentiation"
m (→Lagrange Polynomials) |
m (fix a mistake in the text on deriving the stencils from Taylor series.) |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| + | Often we need to approximate the derivative of a function when we | ||
| + | cannot obtain it analytically. Here we discuss several ways to do this | ||
| + | numerically. | ||
== Taylor Series == | == Taylor Series == | ||
| + | Let's consider the situation where we have samples of a function | ||
| + | <math>f(x)</math> at discrete points <math>\begin{array}{cccc}x_1 & | ||
| + | x_2 & \cdots & x_n\end{array}</math> seperated by spacing | ||
| + | <math>h</math> as depicted in the following figure: | ||
| + | [[Image:uniform_grid_1D.png|thumb|400px|center]] | ||
| + | Consider a [[Taylor_Series|Taylor series]] expansions about some | ||
| + | arbitrary point <math>x_i</math>. Since <math>x_{i+1}-x_i = | ||
| + | x_i-x_{i-1} = h</math> we can write these as follows: | ||
| + | :{| border=1 cellpadding=5 cellspacing=0 style="text-align:left" | ||
| + | ! Approximation location | ||
| + | ! Taylor Series Expansion about <math>x_i</math> | ||
| + | |- | ||
| + | | <math>x_{i+1}</math> | ||
| + | ||<math> | ||
| + | f(x_{i+1}) = f(x_i) | ||
| + | + f^\prime(x_i) h | ||
| + | + \tfrac{1}{2}f^{\prime\prime}(x_i) h^2 | ||
| + | + \tfrac{1}{6}f^{\prime\prime\prime}(x_i) h^3 | ||
| + | + \tfrac{1}{24}f^{(4)}(x_i) h^4 | ||
| + | + \cdots | ||
| + | </math> | ||
| + | |- | ||
| + | | <math>x_{i-1}</math> | ||
| + | ||<math> | ||
| + | f(x_{i-1}) = f(x_i) | ||
| + | - f^\prime(x_i)h | ||
| + | + \tfrac{1}{2}f^{\prime\prime}(x_i)h^2 | ||
| + | - \tfrac{1}{6}f^{\prime\prime\prime}(x_i)h^3 | ||
| + | + \tfrac{1}{24}f^{(4)}(x_i)h^4 | ||
| + | - \cdots | ||
| + | </math> | ||
| + | |} | ||
| + | If we subtract the Taylor series expansion at <math>x_{i-1}</math> | ||
| + | from the one at <math>x_{i+1}</math>, we find | ||
| + | :<math> | ||
| + | f(x_{i+1})-f(x_{i-1}) = 2f^{\prime}(x_i)h + \tfrac{1}{3} f^{\prime\prime\prime}(x_i) h^3 + \cdots | ||
| + | </math> | ||
| + | Now we solve this for <math>f^\prime(x_i)</math> to find | ||
| + | :<math> | ||
| + | f^{\prime}(x_i) = \frac{f(x_{i+1})-f(x_{i-1})}{2h} - \tfrac{1}{6} f^{\prime\prime\prime}(x_i)h^2 - \cdots | ||
| + | </math> | ||
| + | Now if <math>h</math> is small, then the second term (with the | ||
| + | <math>h^2</math> in it) is small and we can approximate the derivative | ||
| + | as | ||
| + | :{|border=2 | ||
| + | |- | ||
| + | |<math> | ||
| + | f^\prime(x_i) = \frac{f(x_{i+1})-f(x_{i-1})}{2h} | ||
| + | </math> | ||
| + | |} | ||
| + | We call this a '''second order approximation''' to | ||
| + | <math>f^\prime(x)</math> because when we truncated the series | ||
| + | approximation to <math>f^\prime(x_i)</math> the largest term there was | ||
| + | of the order of <math>h^2</math>. | ||
| − | + | Note that we now have a way to approximate the derivative of a function if we have the function's values at two locations. | |
| − | + | On a uniform mesh, we can use this technique to generate a variety of | |
| − | + | approximations to derivatives, as summarized in the following table: | |
| − | |||
| − | |||
| − | = | + | {| align=center |
| − | + | | | |
| − | + | {| border=1 cellpadding=5 cellspacing=0 style="text-align:center" | |
| − | {| border= | + | ! Formula for <math> \left. \frac{\mathrm{d} f}{\mathrm{d}x} \right|_{i}</math> |
| − | |||
| − | |||
| − | |||
| − | |||
! Order | ! Order | ||
|- | |- | ||
| − | + | |<math> | |
| − | | <math> | + | \frac{f(x_{i+1})-f(x_{i})}{h}</math> |
| − | | <math>\mathcal{O}\left( | + | ||<math>\mathcal{O}\left( h \right) </math> |
|- | |- | ||
| − | + | |<math> | |
| − | | <math> | + | \frac{f(x_{i})-f(x_{i-1})}{h}</math> |
| − | | <math>\mathcal{O}\left( | + | ||<math>\mathcal{O}\left( h \right) </math> |
|- | |- | ||
| − | + | |<math> | |
| − | + | \frac{f(x_{i+1})-f(x_{i-1})}{2 h}</math> | |
| − | | <math>\mathcal{O}\left( | + | | <math>\mathcal{O}\left(h^2 \right) </math> |
|- | |- | ||
| + | |<math> | ||
| + | \frac{f(x_{i-2}) - 8 f(x_{i-1}) + 8 f(x_{i+1}) - f(x_{i+2})}{12 h} | ||
| + | </math> | ||
| + | ||<math>\mathcal{O}\left( h^4 \right) </math> | ||
| + | |} | ||
| + | || | ||
| + | [[Image:derConverge_uniform_mesh.png|thumb|450px|Error in approximation | ||
| + | of <math>\frac{df}{dx}</math> as a function of the size of the | ||
| + | interval <math>h</math>. Click [[media:der_demo.m|here]] to download | ||
| + | the matlab file that produced this plot.]] | ||
|} | |} | ||
| − | |||
| + | As can be seen in the figure above, higher order approximations result | ||
| + | in significantly lower error for a given spacing <math>h</math>. Note | ||
| + | that for <math>h<10^{-3}</math> the fourth-order approximation is | ||
| + | contaminated by roundoff error. The same would happen for the other | ||
| + | derivative approximations, but at smaller <math>h</math>. | ||
| − | < | + | <!-- jcs need to fill this in |
| − | {| border= | + | {| border=1 cellpadding=5 cellspacing=0 align=center style="text-align:center" |
| − | |+ | + | |+ Some Second Derivative Expressions for a Uniform Mesh |
|- | |- | ||
! Derivative at point <math>i</math> | ! Derivative at point <math>i</math> | ||
! Discrete Representation (uniform mesh) | ! Discrete Representation (uniform mesh) | ||
! Order | ! Order | ||
| − | </ | + | |} |
| + | --> | ||
| + | |||
| + | == Lagrange Polynomials == | ||
| + | |||
| + | Lagrange polynomials, which are commonly used for [[Interpolation#Lagrange_Polynomial_Interpolation|interpolation]], can also be used for differentiation. The formula is | ||
| + | :<math>f^{\prime}(x) = \sum_{k=0}^n y_k L_{k}^{\prime}(x),</math> | ||
| + | where <math>L_{k}^{\prime}(x)</math> is given as | ||
| + | :<math>L_{k}^{\prime}(x) = \left[ \sum_{{j=0}\atop{j\ne k}}^{n} \left( \prod_{ {i=0}\atop{i \ne j,k} }^n (x-x_i) \right) \right] \left[ \prod_{{i=0}\atop{i\ne k}}^{n} (x_k-x_i) \right]^{-1}. </math> | ||
| + | Here <math>n</math> is the order of the polynomial and we require <math>n_p=n+1</math> points to form the Lagrange polynomial. | ||
| + | |||
| + | Here are the results for <var>n = 2, 3, 4</var> | ||
| + | |||
| + | :{| border=1 cellpadding=10 cellspacing=1 | ||
| + | ! | ||
| + | ! <var>n</var>=2 | ||
| + | ! <var>n=3</var> | ||
| + | ! <var>n=4</var> | ||
| + | |- | ||
| + | | <math>L_{0}^{\prime}(x)</math> | ||
| + | | <math>\frac{1}{x_{0}-x_{1}}</math> | ||
| + | | <math>\frac{2x-x_{1}-x_{2}}{(x_{0}-x_{1})(x_{0}-x_{2})}</math> | ||
| + | | <math>\frac{3x^{2}-2x\left(x_{1}+x_{2}+x_{3}\right)+x_{1}\left(x_{2}+x_{3}\right)+x_{2}x_{3}}{\left(x_{0}-x_{1}\right)\left(x_{0}-x_{2}\right)\left(x_{0}-x_{3}\right)}</math> | ||
| + | |- | ||
| + | | <math>L_{1}^{\prime}(x)</math> | ||
| + | | <math>\frac{1}{x_{1}-x_{0}}</math> | ||
| + | | <math>\frac{2x-x_{0}-x_{2}}{(x_{1}-x_{0})(x_{1}-x_{2})}</math> | ||
| + | | <math>-\frac{3x^{2}-2x(x_{0}+x_{2}+x_{3})+x_{0}\left(x_{2}+x_{3}\right)+x_{2}x_{3}}{\left(x_{0}-x_{1}\right)\left(x_{1}-x_{2}\right)\left(x_{1}-x_{3}\right)}</math> | ||
| + | |- | ||
| + | | <math>L_{2}^{\prime}(x)</math> | ||
| + | | | ||
| + | | <math>\frac{2x-x_{0}-x_{1}}{(x_{2}-x_{0})(x_{2}-x_{1})}</math> | ||
| + | | <math>\frac{3x^{2}-2x(x_{0}+x_{1}+x_{3})+x_{0}\left(x_{1}+x_{3}\right)+x_{1}x_{3}}{\left(x_{0}-x_{2}\right)\left(x_{1}-x_{2}\right)\left(x_{2}-x_{3}\right)}</math> | ||
| + | |- | ||
| + | | <math>L_{3}^{\prime}(x)</math> | ||
| + | | | ||
| + | | | ||
| + | |<math>-\frac{3x^{2}-2x(x_{0}+x_{1}+x_{2})+x_{0}\left(x_{1}+x_{2}\right)+x_{1}x_{2}}{\left(x_{0}-x_{3}\right)\left(x_{1}-x_{3}\right)\left(x_{2}-x_{3}\right)}</math> | ||
| + | |} | ||
Latest revision as of 15:56, 26 August 2010
Introduction
Often we need to approximate the derivative of a function when we cannot obtain it analytically. Here we discuss several ways to do this numerically.
Taylor Series
Let's consider the situation where we have samples of a function
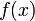 at discrete points
at discrete points 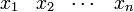 seperated by spacing
seperated by spacing
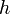 as depicted in the following figure:
as depicted in the following figure:
Consider a Taylor series expansions about some
arbitrary point 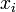 . Since
. Since 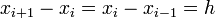 we can write these as follows:
we can write these as follows:
Approximation location Taylor Series Expansion about 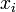
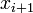
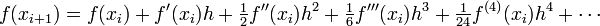
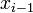
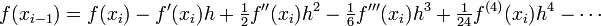
If we subtract the Taylor series expansion at 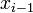 from the one at
from the one at 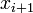 , we find
, we find
Now we solve this for 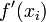 to find
to find
Now if 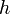 is small, then the second term (with the
is small, then the second term (with the
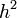 in it) is small and we can approximate the derivative
as
in it) is small and we can approximate the derivative
as
We call this a second order approximation to
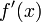 because when we truncated the series
approximation to
because when we truncated the series
approximation to 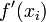 the largest term there was
of the order of
the largest term there was
of the order of 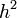 .
.
Note that we now have a way to approximate the derivative of a function if we have the function's values at two locations.
On a uniform mesh, we can use this technique to generate a variety of approximations to derivatives, as summarized in the following table:
|
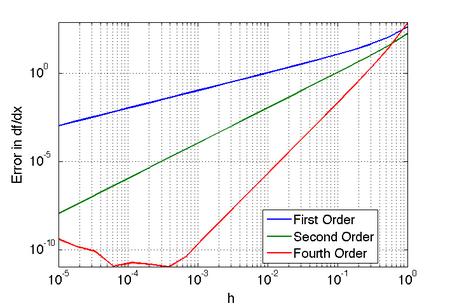 Error in approximation of 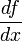 as a function of the size of the interval as a function of the size of the interval 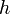 . Click here to download the matlab file that produced this plot. . Click here to download the matlab file that produced this plot. |
As can be seen in the figure above, higher order approximations result
in significantly lower error for a given spacing 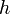 . Note
that for
. Note
that for 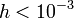 the fourth-order approximation is
contaminated by roundoff error. The same would happen for the other
derivative approximations, but at smaller
the fourth-order approximation is
contaminated by roundoff error. The same would happen for the other
derivative approximations, but at smaller 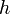 .
.
Lagrange Polynomials
Lagrange polynomials, which are commonly used for interpolation, can also be used for differentiation. The formula is
where 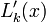 is given as
is given as
Here 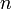 is the order of the polynomial and we require
is the order of the polynomial and we require 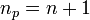 points to form the Lagrange polynomial.
points to form the Lagrange polynomial.
Here are the results for n = 2, 3, 4
n=2 n=3 n=4 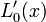
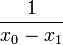
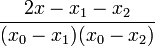
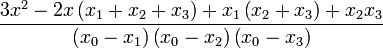
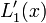
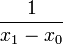
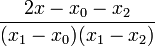
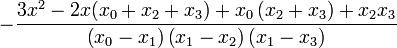
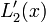
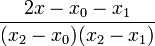
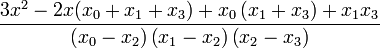
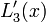
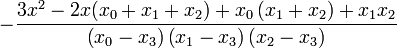
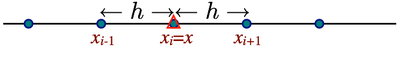
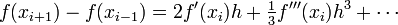
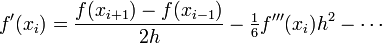
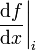
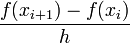
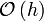
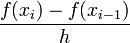
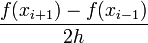
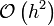
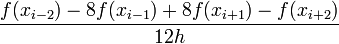
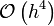
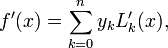
![L_{k}^{\prime}(x) = \left[ \sum_{{j=0}\atop{j\ne k}}^{n} \left( \prod_{ {i=0}\atop{i \ne j,k} }^n (x-x_i) \right) \right] \left[ \prod_{{i=0}\atop{i\ne k}}^{n} (x_k-x_i) \right]^{-1}.](/wiki/images/math/3/c/c/3cced1f629b2f0354163c2308a6df53c.png)