Difference between revisions of "Numerical Differentiation"

Revision as of 20:55, 2 July 2008

Lagrange polynomials, which are commonly used for interpolation, can also be used for differentiation.

**Some First Derivative Expressions for a Uniform Mesh**
Derivative at point 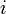$i$	Discrete Representation (uniform mesh)	Order
Forward Difference	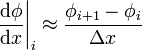$\left. \frac{\mathrm{d}\phi}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i+1}-\phi_{i}}{\Delta x}$	$\mathcal{O}\left(\Delta x \right)$
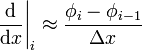
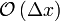
Backward Difference	$\left. \frac{\mathrm{d}}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i}-\phi_{i-1}}{\Delta x}$	$\mathcal{O}\left(\Delta x \right)$
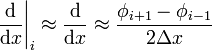
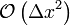
Central Difference	$\left. \frac{\mathrm{d}}{\mathrm{d}x} \right\|_{i} \approx\frac{\mathrm{d}}{\mathrm{d}x} \approx \frac{\phi_{i+1}-\phi_{i-1}}{2\Delta x}$	$\mathcal{O}\left(\Delta x^2 \right)$

**Some Second Derivative Expressions for a Uniform Mesh**
Derivative at point 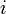$i$	Discrete Representation (uniform mesh)	Order

@@ Line 4: / Line 4: @@
 == Taylor Series ==
@@ Line 9: / Line 10: @@
 == Lagrange Polynomials ==
+Lagrange polynomials, which are commonly used for [[interpolation]], can also be used for differentiation.