Difference between revisions of "Numerical Differentiation"

Revision as of 09:57, 15 July 2008

Lagrange polynomials, which are commonly used for interpolation, can also be used for differentiation. The formula is

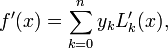
f^{\prime}(x) = \sum_{k=0}^n y_k L_{k}^{\prime}(x),

where 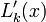$L_{k}^{\prime}(x)$ is given as

L_{k}^{\prime}(x) = \left[ \sum_{{i=0} \atop {i\ne k}}^{n} (x-x_i) \right] \left[ \prod_{{i=0}\atop{i\ne k}}^{n} (x_i-x_k) \right]^{-1}.

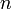Here $n$ is the order of the polynomial and we require 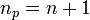$n_p=n+1$ points to form the Lagrange polynomial.

**Some First Derivative Expressions for a Uniform Mesh**
Derivative at point 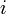$i$	Discrete Representation (uniform mesh)	Order
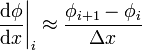
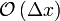
Forward Difference	$\left. \frac{\mathrm{d}\phi}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i+1}-\phi_{i}}{\Delta x}$	$\mathcal{O}\left(\Delta x \right)$
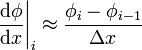
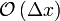
Backward Difference	$\left. \frac{\mathrm{d}\phi}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i}-\phi_{i-1}}{\Delta x}$	$\mathcal{O}\left(\Delta x \right)$
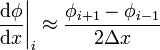
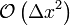
Central Difference	$\left. \frac{\mathrm{d\phi}}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i+1}-\phi_{i-1}}{2\Delta x}$	$\mathcal{O}\left(\Delta x^2 \right)$

**Some Second Derivative Expressions for a Uniform Mesh**
Derivative at point 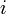$i$	Discrete Representation (uniform mesh)	Order

@@ Line 15: / Line 15: @@
 where <math>L_{k}^{\prime}(x)</math> is given as
 <center><math>L_{k}^{\prime}(x) = \left[ \sum_{{i=0} \atop {i\ne k}}^{n} (x-x_i) \right] \left[ \prod_{{i=0}\atop{i\ne k}}^{n} (x_i-x_k) \right]^{-1}. </math></center>
+Here <math>n</math> is the order of the polynomial and we require <math>n_p=n+1</math> points to form the Lagrange polynomial.
 == Tables for Derivatives on Uniform Grids ==