Difference between revisions of "Numerical Differentiation"

Revision as of 09:24, 7 July 2008

Lagrange polynomials, which are commonly used for interpolation, can also be used for differentiation.

**Some First Derivative Expressions for a Uniform Mesh**
Derivative at point 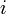$i$	Discrete Representation (uniform mesh)	Order
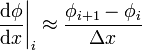
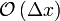
Forward Difference	$\left. \frac{\mathrm{d}\phi}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i+1}-\phi_{i}}{\Delta x}$	$\mathcal{O}\left(\Delta x \right)$
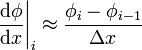
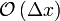
Backward Difference	$\left. \frac{\mathrm{d}\phi}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i}-\phi_{i-1}}{\Delta x}$	$\mathcal{O}\left(\Delta x \right)$
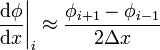
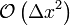
Central Difference	$\left. \frac{\mathrm{d\phi}}{\mathrm{d}x} \right\|_{i} \approx \frac{\phi_{i+1}-\phi_{i-1}}{2\Delta x}$	$\mathcal{O}\left(\Delta x^2 \right)$

**Some Second Derivative Expressions for a Uniform Mesh**
Derivative at point 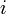$i$	Discrete Representation (uniform mesh)	Order

@@ Line 31: / Line 31: @@
 |-
 | Backward Difference
-| <math> \left. \frac{\mathrm{d}}{\mathrm{d}x} \right|_{i} \approx \frac{\phi_{i}-\phi_{i-1}}{\Delta x}</math>
+| <math> \left. \frac{\mathrm{d}\phi}{\mathrm{d}x} \right|_{i} \approx \frac{\phi_{i}-\phi_{i-1}}{\Delta x}</math>
 | <math>\mathcal{O}\left(\Delta x \right) </math>
 |-
 | Central Difference
-| | <math> \left. \frac{\mathrm{d}}{\mathrm{d}x} \right|_{i} \approx\frac{\mathrm{d}}{\mathrm{d}x} \approx \frac{\phi_{i+1}-\phi_{i-1}}{2\Delta x}</math>
+| | <math> \left. \frac{\mathrm{d\phi}}{\mathrm{d}x} \right|_{i} \approx \frac{\phi_{i+1}-\phi_{i-1}}{2\Delta x}</math>
 | <math>\mathcal{O}\left(\Delta x^2 \right) </math>
 |-